题目内容
函数y=tan( +
+ )的周期为________单调区间为________.
)的周期为________单调区间为________.
2 (- +2k,
+2k, +2k)(k∈Z)
+2k)(k∈Z)
分析:根据正切函数的周期公式T= 可得函数的周期为2,根据正切函数的单调区间(-
可得函数的周期为2,根据正切函数的单调区间(- ,
, ),利用整体思想利用
),利用整体思想利用 +
+ 代替x的位置进而得到函数的单调区间.
代替x的位置进而得到函数的单调区间.
解答:因为函数为y=tan( +
+ ),
),
所以周期T= =
=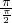 =2.
=2.
因为函数y=tanx的单调区间为(- ,
, ),
),
所以- <
< +
+ <
< ,解得:-
,解得:- +2k<x<
+2k<x< +2k,k∈Z
+2k,k∈Z
所以函数y=tan( +
+ )的单调区间为(-
)的单调区间为(- +2k,
+2k, +2k)(k∈Z).
+2k)(k∈Z).
故答案为:2,(- +2k,
+2k, +2k)(k∈Z).
+2k)(k∈Z).
点评:解决此类问题的关键是熟练掌握正切函数的有关性质,如周期性、单调性与奇偶性等性质.
 +2k,
+2k, +2k)(k∈Z)
+2k)(k∈Z)分析:根据正切函数的周期公式T=
 可得函数的周期为2,根据正切函数的单调区间(-
可得函数的周期为2,根据正切函数的单调区间(- ,
, ),利用整体思想利用
),利用整体思想利用 +
+ 代替x的位置进而得到函数的单调区间.
代替x的位置进而得到函数的单调区间.解答:因为函数为y=tan(
 +
+ ),
),所以周期T=
 =
=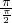 =2.
=2.因为函数y=tanx的单调区间为(-
 ,
, ),
),所以-
 <
< +
+ <
< ,解得:-
,解得:- +2k<x<
+2k<x< +2k,k∈Z
+2k,k∈Z所以函数y=tan(
 +
+ )的单调区间为(-
)的单调区间为(- +2k,
+2k, +2k)(k∈Z).
+2k)(k∈Z).故答案为:2,(-
 +2k,
+2k, +2k)(k∈Z).
+2k)(k∈Z).点评:解决此类问题的关键是熟练掌握正切函数的有关性质,如周期性、单调性与奇偶性等性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
关于函数y=tan(2x-
),下列说法正确的是( )
| π |
| 3 |
| A、是奇函数 | ||
| B、最小正周期为π | ||
C、(
| ||
D、其图象由y=tan2x的图象右移
|