题目内容
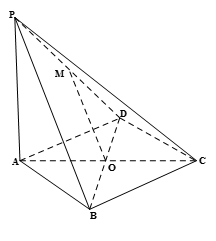
如图,在四棱锥 中,
中, 底面
底面 ,
, ,
, ,
,
 ,
, 是
是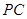 的中点.
的中点.
(Ⅰ)证明: ;
;
(Ⅱ)证明: 平面
平面 ;
;
(Ⅲ)求二面角 的正切值.
的正切值.
(Ⅰ)证明:见解析。(Ⅱ)证明:见解析。(Ⅲ)二面角 的正切值是
的正切值是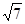 .
.
解析试题分析:(1)根据题目中的线面的垂直性质定理得到线线垂直的证明。
(2)利用上一问的结论和线面垂直的判定定理得到证明。
(3)结合三垂线定理作出二面角的平面角,然后借助于三角形来求解大小。
(Ⅰ)证明:在四棱锥 中,因
中,因 底面
底面 ,
,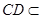 平面
平面 ,故
,故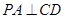 .
.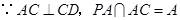 ,
,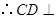 平面
平面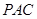 .
.
而 平面
平面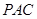 ,
,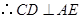 .…………………………………………(4分)
.…………………………………………(4分)
(Ⅱ)证明:由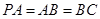 ,
, ,可得
,可得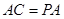 .
. 是
是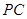 的中点,
的中点,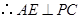 .
.
由(Ⅰ)知, ,且
,且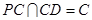 ,所以
,所以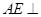 平面
平面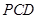 .
.
而 平面
平面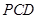 ,
,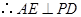 .
.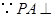 底面
底面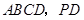 在底面
在底面 内的射影是
内的射影是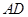 ,
,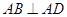 ,
, .
.
又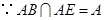 ,综上得
,综上得 平面
平面 .………………………………(8分)
.………………………………(8分)
(Ⅲ)解法一:过点 作
作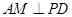 ,垂足为
,垂足为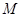 ,连结
,连结 .则(Ⅱ)知,
.则(Ⅱ)知,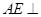 平面
平面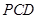 ,
,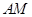 在平面
在平面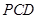 内的射影是
内的射影是 ,则
,则 .
.
因此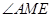 是二面角
是二面角 的平面角.
的平面角.
由已知,得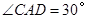 .设
.设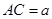 ,
,
可得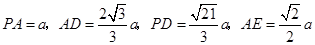 .
.
在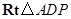 中,
中,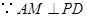 ,
,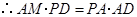 ,
,
则 .
.
在 中,
中,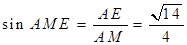 .
.
所以二面角 的正切值为
的正切值为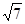 .……………………………………(12分)
.……………………………………(12分)
解法二:由题设 底面
底面 ,
,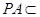 平面
平面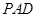 ,则平面
,则平面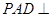 平面
平面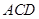 ,交线为
,交线为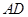 .
.
过点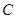 作
作 ,垂足为
,垂足为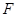 ,故
,故 平面
平面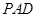 .过点
.过点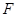 作
作
练习册系列答案
相关题目
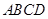 ⊥平面
⊥平面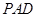 ,
, 是直角三角形,
是直角三角形,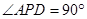 ,四边形
,四边形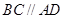 ,
,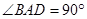 ,
, ,且
,且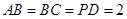 ,
,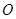 是
是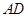 的中点,
的中点,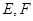 分别是
分别是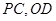 的中点.
的中点. 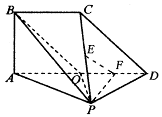
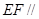 平面
平面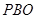 ;
;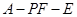 的正切值.
的正切值.
 平面
平面 ;
;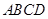 中,
中,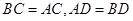 ,
,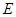 是
是 的中点.
的中点.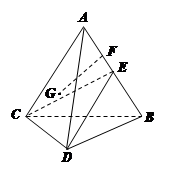
 平面
平面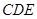 ;
;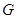 为
为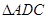 的重心,
的重心,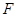 是线段
是线段 上一点,且
上一点,且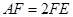 .求证:
.求证: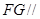 平面
平面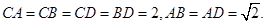

 平面BCD;
平面BCD;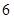 ,在四棱锥
,在四棱锥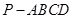 中,
中,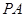
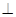 平面
平面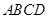 ,底面
,底面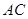 与
与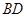 的交点,
的交点,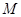 是
是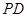 的中点,
的中点,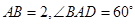 .
.
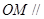 平面
平面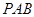 ;
;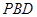
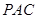 ;
;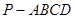 的体积等于
的体积等于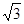 时,求
时,求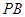 的长.
的长.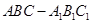 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中,  ,
, 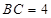 ,
, 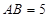 ,
,  ,点
,点 是
是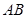 的中点.
的中点. 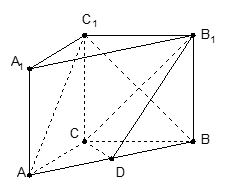
 ∥平面
∥平面 ;
; 中,
中,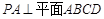 ,
,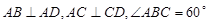 ,且
,且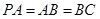 ,E是PC的中点.
,E是PC的中点.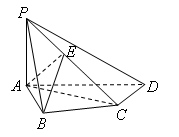
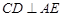 ;
; 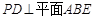 ;
;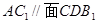 ;
;