题目内容
已知数列{ }是等比数列,且a2=18,a5=1215.
}是等比数列,且a2=18,a5=1215.
(I)求数列{an}的通项an;
(Ⅱ)求数列{an}的前n项和Sn.
解(I):由题意得:数列{ }是等比数列,设该数列的公比为q,
}是等比数列,设该数列的公比为q,
则 =
=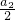 •q3…2′
•q3…2′
又a2=18,a5=1215,
∴q3=27,q=3…4′
∴ =
=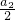 •qn-2,
•qn-2,
∴an=n•3n…6′
(Ⅱ)设Sn=a1+a2+a3+…+an,
则Sn=3+2×32+3×33+…+n•3n,①
∴3Sn=32+2×33+…+(n-1)•3n+n•3n+1②…8′
①-②
-2Sn=3+32+33+…+3n-n•3n+1…10′
=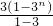 -n•3n+1
-n•3n+1
= •3n+1-
•3n+1- ,
,
∴Sn=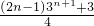 …12′
…12′
分析:(Ⅰ)由数列{ }是等比数列,设该数列的公比为q,则
}是等比数列,设该数列的公比为q,则 =
=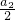 •q3,又a2=18,a5=1215,可求得q=3,从而可求得an.
•q3,又a2=18,a5=1215,可求得q=3,从而可求得an.
(Ⅱ)设Sn=a1+a2+a3+…+an,则Sn=3+2×32+3×33+…+n•3n,利用错位相减法即可求得Sn的值.
点评:本题考查数列的求和,着重考查等比数列的通项公式与错位相减法求和,求得an=n•3n是关键,属于中档题.
 }是等比数列,设该数列的公比为q,
}是等比数列,设该数列的公比为q,则
 =
=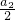 •q3…2′
•q3…2′又a2=18,a5=1215,
∴q3=27,q=3…4′
∴
 =
=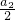 •qn-2,
•qn-2,∴an=n•3n…6′
(Ⅱ)设Sn=a1+a2+a3+…+an,
则Sn=3+2×32+3×33+…+n•3n,①
∴3Sn=32+2×33+…+(n-1)•3n+n•3n+1②…8′
①-②
-2Sn=3+32+33+…+3n-n•3n+1…10′
=
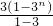 -n•3n+1
-n•3n+1=
 •3n+1-
•3n+1- ,
,∴Sn=
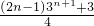 …12′
…12′分析:(Ⅰ)由数列{
 }是等比数列,设该数列的公比为q,则
}是等比数列,设该数列的公比为q,则 =
=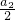 •q3,又a2=18,a5=1215,可求得q=3,从而可求得an.
•q3,又a2=18,a5=1215,可求得q=3,从而可求得an.(Ⅱ)设Sn=a1+a2+a3+…+an,则Sn=3+2×32+3×33+…+n•3n,利用错位相减法即可求得Sn的值.
点评:本题考查数列的求和,着重考查等比数列的通项公式与错位相减法求和,求得an=n•3n是关键,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 0,b
0,b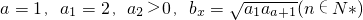 .且{bx}是以
.且{bx}是以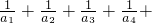 …
…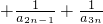 .
. .且{bx}是以
.且{bx}是以 …
… .
.