题目内容
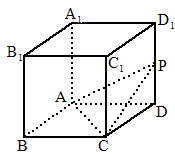
如下图所示,已知正方体ABCD-A1B1C1D1中,E、F、G分别是棱AB、BC、BB1上三点,且BE=BF=BG,求证:BD1⊥平面EFG.
答案:
解析:
提示:
解析:
|
证明:∵四边形ABCD为正方形,且BE=BF, ∴EF∥AC 又∵AC⊥BD, ∴EF⊥BD 而EF⊥DD1,则知EF⊥面BDD1. ∴BD1⊥EF. 同理,BD1⊥EG. ∴BD1⊥平面EFG. |
提示:
|
证明线面垂直,常转化为证明线线垂直.本题中只要证得BD1⊥EF,则同理可证BD1⊥EG,进而得到结论. |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目








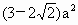
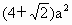
 侧棱
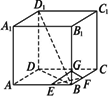
侧棱 的中点,过D作平面PAC的垂线,则该垂线与正方体表面的另一个交点Q(不同于D)的位置在________.
的中点,过D作平面PAC的垂线,则该垂线与正方体表面的另一个交点Q(不同于D)的位置在________.