题目内容
如图,△BCD所在的平面垂直于正△ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E,F分别为DB,CB的中点,
(1)证明PE∥平面ABC;
(2)证明AE⊥BC;
(3)求直线PF与平面BCD所成的角的大小.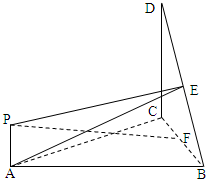
(1)证明PE∥平面ABC;
(2)证明AE⊥BC;
(3)求直线PF与平面BCD所成的角的大小.

(1)连接EF,AF

∵平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,CD⊥BC
∴CD⊥平面ABC,结合PA⊥平面ABC,可得PA∥CD
∵EF是△BCD的中位线,∴EF∥CD且EF=
CD
∵PA∥CD且PA=
CD,∴四边形PAFE是平行四边形,可得PE∥AF,
∵PE?平面ABC,AF?平面ABC,∴PE∥平面ABC;
(2)∵PA⊥平面ABC,BC?平面ABC,∴BC⊥PA
∵正△ABC中,F为BC中点,∴BC⊥AF
∵AF、PA是平面PAFE内的相交直线,
∴BC⊥平面PAFE,
∵AF?平面PAFE,∴AE⊥BC;
(3)∵平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,AF⊥BC
∴AF⊥平面BCD,结合PE∥AF可得PE⊥平面BCD,
因此,∠PFE就是直线PF与平面BCD所成的角
∵正△ABC中,F为BC中点,∴AF=
BC,可得PE=
BC,
又∵△BCD的中位线FE=
CD,CD=BC,∴FE=
BC
因此RtPEF中,tan∠PFE=
=
,可得∠PFE=60°
即直线PF与平面BCD所成的角的大小为60°.

∵平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,CD⊥BC
∴CD⊥平面ABC,结合PA⊥平面ABC,可得PA∥CD
∵EF是△BCD的中位线,∴EF∥CD且EF=
| 1 |
| 2 |
∵PA∥CD且PA=
| 1 |
| 2 |
∵PE?平面ABC,AF?平面ABC,∴PE∥平面ABC;
(2)∵PA⊥平面ABC,BC?平面ABC,∴BC⊥PA
∵正△ABC中,F为BC中点,∴BC⊥AF
∵AF、PA是平面PAFE内的相交直线,
∴BC⊥平面PAFE,
∵AF?平面PAFE,∴AE⊥BC;
(3)∵平面BCD⊥平面ABC,平面BCD∩平面ABC=BC,AF⊥BC
∴AF⊥平面BCD,结合PE∥AF可得PE⊥平面BCD,
因此,∠PFE就是直线PF与平面BCD所成的角
∵正△ABC中,F为BC中点,∴AF=
| ||
| 2 |
| ||
| 2 |
又∵△BCD的中位线FE=
| 1 |
| 2 |
| 1 |
| 2 |
因此RtPEF中,tan∠PFE=
| PE |
| FE |
| 3 |
即直线PF与平面BCD所成的角的大小为60°.

练习册系列答案
相关题目
 (2011•宝坻区一模)如图,△BCD所在的平面垂直于正△ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E,F分别为DB,CB的中点,
(2011•宝坻区一模)如图,△BCD所在的平面垂直于正△ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E,F分别为DB,CB的中点,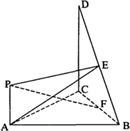
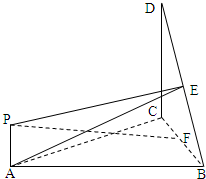 如图,△BCD所在的平面垂直于正△ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E,F分别为DB,CB的中点,
如图,△BCD所在的平面垂直于正△ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E,F分别为DB,CB的中点, 如图,△BCD所在的平面垂直于正△ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E,F分别为DB,CB的中点,
如图,△BCD所在的平面垂直于正△ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E,F分别为DB,CB的中点,