题目内容
函数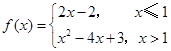 的图象和函数
的图象和函数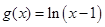 的图象的交点个数是 。
的图象的交点个数是 。
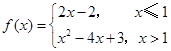 的图象和函数
的图象和函数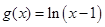 的图象的交点个数是 。
的图象的交点个数是 。2
试题分析:在同一坐标系内作出
 和
和 的图象,对于
的图象,对于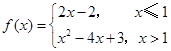 ,
,当
 时,它的图象是直线
时,它的图象是直线 位于直线
位于直线 左侧的部分;当
左侧的部分;当 时,它的图象是抛物线
时,它的图象是抛物线 位于直线
位于直线 右侧部分,对于
右侧部分,对于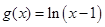 ,它的图象是对数函数
,它的图象是对数函数 的图象右移一个单位而得,经过定点
的图象右移一个单位而得,经过定点 且在直线
且在直线 右侧,以
右侧,以 为渐近线呈增函数趋势,∵当
为渐近线呈增函数趋势,∵当 时,点
时,点 位于抛物线张口以内,且
位于抛物线张口以内,且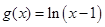 经过该点,∴在直线
经过该点,∴在直线 右侧,两图象有两个交点
右侧,两图象有两个交点因为函数
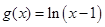 上所有的点都在
上所有的点都在 右侧,故当
右侧,故当 时,两图象没有公式点,综上所述,函数
时,两图象没有公式点,综上所述,函数 图象和函数
图象和函数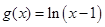 的图象有且仅有两个交点,故答案为:2.
的图象有且仅有两个交点,故答案为:2.

练习册系列答案
相关题目
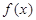 是
是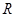 上的增函数,
上的增函数,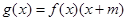 ,已知
,已知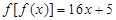 .
.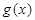 在
在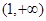 单调递增,求实数
单调递增,求实数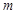 的取值范围;
的取值范围;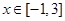 时,
时,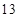 ,求实数
,求实数 ,且两函数定义域均为
,且两函数定义域均为 ,
, 在定义域内的图像,并求
在定义域内的图像,并求 的值域.(5分)
的值域.(5分)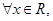
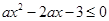 恒成立”是真命题,则实数a的取值范围是 .
恒成立”是真命题,则实数a的取值范围是 . 对任意实数
对任意实数 有
有 成立,若当
成立,若当 时
时 恒成立,则
恒成立,则 的取值范围是_________.
的取值范围是_________.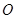 为坐标原点,给定一个定点
为坐标原点,给定一个定点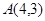 ,而点
,而点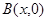 在
在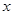 正半轴上移动,
正半轴上移动,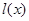 表示
表示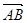 的长,则
的长,则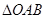 中两边长的比值
中两边长的比值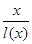 的最大值为 .
的最大值为 .