题目内容
2．在底面半径为R，高为h的圆锥内有一内接圆柱，则内接圆柱的圆柱的高为$\frac{h}{2}$时，其侧面积最大值为$\frac{1}{2}$πRh．分析 设所求的圆柱的底面半径为r．它的侧面积S=2πrx，mh $\frac{r}{R}$=$\frac{h-x}{h}$，得r=R-$\frac{R}{h}$•x，从而得到圆柱的侧面积S是关于x的二次函数S=-$\frac{2πR}{h}$x2+2πRx，由此能求出结果．
解答 解：圆锥及其内接圆柱的轴截面如图所示．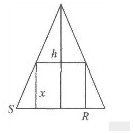
设所求的圆柱的底面半径为r．它的侧面积S=2πrx，
∵$\frac{r}{R}$=$\frac{h-x}{h}$，∴r=R-$\frac{R}{h}$•x，
∴S=2πRx-$\frac{2πR}{h}$x2，
圆柱的侧面积S是关于x的二次函数：
S=-$\frac{2πR}{h}$x2+2πRx，
∵S的表达式中x2的系数小于0，
∴这个二次函数有最大值，
这时圆柱的高x=$\frac{h}{2}$，
即当圆柱的高是已知圆锥的一半时，它的侧面积最大．
侧面积的最大值为Smax=-$\frac{2πR}{h}•（\frac{h}{2}）^{2}$+2$πR•\frac{h}{2}$=$\frac{1}{2}πRh$．
故答案为：$\frac{h}{2}$，$\frac{1}{2}πRh$．
点评 本题考查圆锥内接圆柱的侧面积的最大值的求法，是中档题，解题时要认真审题，注意二次函数的性质的合理运用．
练习册系列答案
相关题目
13．
已知函数f（x）的定义域[-1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图所示．
（1）方程f[f（x）]=0的不等实根的个数为2；
（2）方程f[f（x）]-a=0，a∈[-1，2]的不等实根的个数构成的集合为{1，2，4}．
已知函数f（x）的定义域[-1，5]，部分对应值如表，f（x）的导函数y=f′（x）的图象如图所示．| x | -1 | 0 | 2 | 4 | 5 |
| y | 1 | 2 | 0 | 2 | 1 |
（2）方程f[f（x）]-a=0，a∈[-1，2]的不等实根的个数构成的集合为{1，2，4}．
10．如果有下列这段伪代码，那么将执行多少次循环（ ）
sum←0
For x=1to 10
sum←sum+x
If sum＞10 then
Exit For
End if
Next．
sum←0
For x=1to 10
sum←sum+x
If sum＞10 then
Exit For
End if
Next．
| A． | 4次 | B． | 5次 | C． | 7次 | D． | 10次 |
17．下列说法错误的是（ ）
| A． | 若p：?x∈R，x2-x+1=0，则￢p：?x∈R，x2-x+1≠0 | |
| B． | “sinθ=$\frac{1}{2}$”是“θ=30°或150°”的充分不必要条件 | |
| C． | 命题“若a=0，则ab=0”的否命题是“若a≠0，则ab≠0” | |
| D． | 已知p：?x∈R，cosx=1，q：?x∈R，x2-x+1＞0，则“p∧（￢q）”为假命题 |
7．已知A={-1，2}，B={x|mx+1=0}，若A∪B=A，则实数m的取值所成的集合是（ ）
| A． | $\left\{{-1，\frac{1}{2}}\right\}$ | B． | $\left\{{-\frac{1}{2}，1}\right\}$ | C． | $\left\{{-1，0，\frac{1}{2}}\right\}$ | D． | $\left\{{-\frac{1}{2}，0，1}\right\}$ |