题目内容
设a>0且a≠1,f(x)=loga(x+| x2-1 |
(1)求函数f(x)的反函数f-1(x)及其定义域.(2)若f-1(n)<
| 3n+3-n |
| 2 |
分析:(1)、求出函数f(x)的反函数f-1(x)后,分a>1和0<a<1两种情况求反函数f-1(x)的定义域.
(2)、把反函数中的x换成n,然后按不等多的运算法则进行求解.
(2)、把反函数中的x换成n,然后按不等多的运算法则进行求解.
解答:解(Ⅰ)∵f(x)=loga(x+
)(x≥1),
∴ay=x+
(x≥1),∴
=ay-x,
∴a2y-2ayx+1=0,(x≥1),∴x=
=
,
互换x,y得f-1(x)=
.
当a>1时,定义域为[0,+∞)
当0<a<1时,定义域为(-∞,0]
(Ⅱ)f-1(n)<
(n∈N*),由(1)中反函数f-1(x)定义域可得a>1,
即
<
即(an-3n)[(3a)n-1]<0
即
∴
<a<3,
又由a>1,则a的取值范围是(1,3).
| x2-1 |
∴ay=x+
| x2-1 |
| x2-1 |
∴a2y-2ayx+1=0,(x≥1),∴x=
| a2y+1 |
| 2ay |
| ay+a-y |
| 2 |
互换x,y得f-1(x)=
| ax+a-x |
| 2 |
当a>1时,定义域为[0,+∞)
当0<a<1时,定义域为(-∞,0]
(Ⅱ)f-1(n)<
| 3n+3-n |
| 2 |
即
| an+a-n |
| 2 |
| 3n+3-n |
| 2 |
即(an-3n)[(3a)n-1]<0
即
|
∴
| 1 |
| 3 |
又由a>1,则a的取值范围是(1,3).
点评:根据指数函数和对数函数的性质正确求出函数f(x)的反函数f-1(x)是解题的关键.

练习册系列答案
相关题目
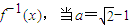 时,比较f-1[g(x)]与-1的大小,证明你的结论;
时,比较f-1[g(x)]与-1的大小,证明你的结论;