题目内容
已知f(x)=xlnx,g(x)=-x2+ax-3.(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.
【答案】分析:(1)f'(x)=lnx+1,当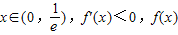 单调递减,当
单调递减,当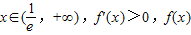 单调递增,由此进行分类讨论,能求出函数f(x)在[t,t+2](t>0)上的最小值.
单调递增,由此进行分类讨论,能求出函数f(x)在[t,t+2](t>0)上的最小值.
(2)由2xlnx≥-x2+ax-3,知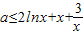 ,设
,设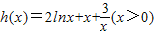 ,则
,则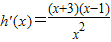 ,由此入手能够求出实数a的取值范围.
,由此入手能够求出实数a的取值范围.
解答:解:(1)∵f(x)=xlnx,
∴f'(x)=lnx+1,…(1分)
当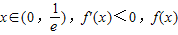 单调递减,
单调递减,
当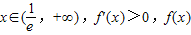 单调递增,…(3分)
单调递增,…(3分)
①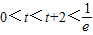 ,没有最小值; …(4分)
,没有最小值; …(4分)
②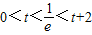 ,即
,即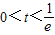 时,
时,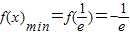 ;…(5分)
;…(5分)
③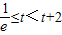 ,即
,即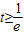 时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt…(6分)
时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt…(6分)
所以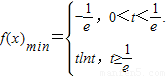 …(7分)
…(7分)
(2)2xlnx≥-x2+ax-3,则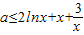 ,…(9分)
,…(9分)
设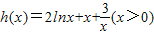 ,
,
则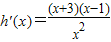 ,…(10分)
,…(10分)
①x∈(0,1),h'(x)<0,h(x)单调递减,
②x∈(1,+∞),h'(x)>0,h(x)单调递增,
所以h(x)min=h(1)=4,
对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
∵g(x)=-x2+ax-3.所以a≤h(x)min=4;…(13分)
点评:本题考查求函数f(x)在[t,t+2](t>0)上的最小值;对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.解题时要认真审题,注意导数性质的合理运用.
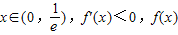 单调递减,当
单调递减,当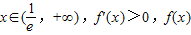 单调递增,由此进行分类讨论,能求出函数f(x)在[t,t+2](t>0)上的最小值.
单调递增,由此进行分类讨论,能求出函数f(x)在[t,t+2](t>0)上的最小值.(2)由2xlnx≥-x2+ax-3,知
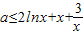 ,设
,设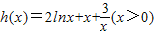 ,则
,则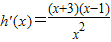 ,由此入手能够求出实数a的取值范围.
,由此入手能够求出实数a的取值范围.解答:解:(1)∵f(x)=xlnx,
∴f'(x)=lnx+1,…(1分)
当
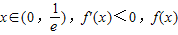 单调递减,
单调递减,当
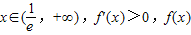 单调递增,…(3分)
单调递增,…(3分)①
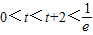 ,没有最小值; …(4分)
,没有最小值; …(4分)②
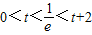 ,即
,即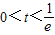 时,
时,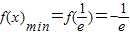 ;…(5分)
;…(5分)③
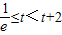 ,即
,即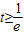 时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt…(6分)
时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt…(6分)所以
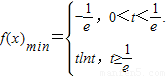 …(7分)
…(7分)(2)2xlnx≥-x2+ax-3,则
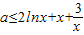 ,…(9分)
,…(9分)设
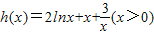 ,
,则
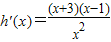 ,…(10分)
,…(10分)①x∈(0,1),h'(x)<0,h(x)单调递减,
②x∈(1,+∞),h'(x)>0,h(x)单调递增,
所以h(x)min=h(1)=4,
对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
∵g(x)=-x2+ax-3.所以a≤h(x)min=4;…(13分)
点评:本题考查求函数f(x)在[t,t+2](t>0)上的最小值;对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目