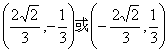题目内容
(06年重庆卷理)(13分)
如图,在四棱锥![]() 中,
中,![]() 底面ABCD,
底面ABCD,![]() 为直角,
为直角,![]() ,
,![]() E、F分别为
E、F分别为![]() 、
、![]() 中点。
中点。
(I)试证:![]() 平面
平面![]() ;
;
(II)高![]() ,且二面角
,且二面角 ![]() 的平面角大小
的平面角大小![]() ,求
,求![]() 的取值范围。
的取值范围。
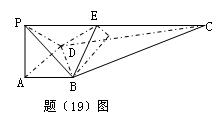
解析:(I)证:由已知![]() 且
且![]() 为直角。故ABFD是矩形。从而
为直角。故ABFD是矩形。从而![]() 。又
。又![]() 底面ABCD,
底面ABCD,![]() ,故由三垂线定理知
,故由三垂线定理知![]() D
D ![]() 中,E、F分别为PC、CD的中点,故EF//PD,从而
中,E、F分别为PC、CD的中点,故EF//PD,从而![]() ,由此得
,由此得![]() 面BEF。
面BEF。
(II)连接AC交BF于G,易知G为AC的中点,连接EG,则在![]() 中易知EG//PA。又因PA
中易知EG//PA。又因PA![]() 底面ABCD,故EG
底面ABCD,故EG![]() 底面ABCD。在底面ABCD中,过G作GH
底面ABCD。在底面ABCD中,过G作GH![]() BD。垂足为H,连接EH,由三垂线定理知EH
BD。垂足为H,连接EH,由三垂线定理知EH![]() BD。从而
BD。从而![]() 为二面角E-BD-C的平面角。
为二面角E-BD-C的平面角。
设![]()
以下计算GH,考虑底面的平面图(如答(19)图2)。连结GD,因![]()
故GH=![]() .在
.在![]() 。而
。而![]()
![]() 。因此,
。因此,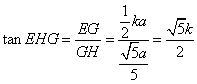 。由
。由![]() 知
知![]() 是锐角。故要使
是锐角。故要使 ![]()
![]() ,必须
,必须![]() ,解之得,中的取值范围为
,解之得,中的取值范围为![]()

练习册系列答案
相关题目
 的展开式中各项系数之和为64,则展开式的常数项为( )
的展开式中各项系数之和为64,则展开式的常数项为( )
 (D)
(D)