题目内容
(理)如图,A、B、C是表面积为48π的球面上的点,且AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成角的大小是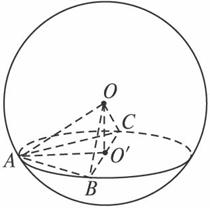
A.arccos![]() B.arccos
B.arccos![]() C.arccos
C.arccos![]() D.arccos
D.arccos![]()
(文)如图,A、B、C是表面积为48π的球面上的点,且AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成角的余弦值是
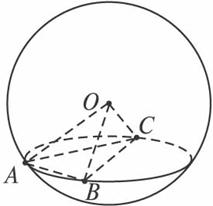
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
答案:D ∵AB=2,BC=4,∠ABC=60°,

∴AC2=AB2+BC2-2AB·BC·cos∠ABC=4+16-2×2×4×![]() =12.
=12.
∴△BAC为直角三角形,∠BAC=90°.
∴截面ABC的圆心O′为BC的中点,AO′=![]() BC=2.又球的表面积为48π=4πR2,
BC=2.又球的表面积为48π=4πR2,
∴R=![]() .又∵∠OO′A=90°,∠OAO′为AO与面ABC所成的角,
.又∵∠OO′A=90°,∠OAO′为AO与面ABC所成的角,
∴cos∠OAO′=![]() .∴理为arccos
.∴理为arccos![]() ,文为
,文为![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 (理)如图所示,一只蚂蚁在一直角边长为1cm的等腰直角三角形ABC(∠B为直角)的边上爬行,则蚂蚁距A点不超过1cm的概率为
(理)如图所示,一只蚂蚁在一直角边长为1cm的等腰直角三角形ABC(∠B为直角)的边上爬行,则蚂蚁距A点不超过1cm的概率为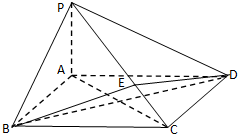 (理)如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点 E在线段PC上,设
(理)如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点 E在线段PC上,设 (理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足