题目内容
已知数列{an},{bn}与函数f(x),g(x),x∈R满足条件:an=bn,f(bn)=g(bn+1)(n∈N*)。
(1)若f(x)≥tx+1,t≠0,t≠2,g(x)=2x,f(b)≠g(b),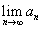 存在,求
存在,求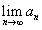 的值;
的值;
(2)若函数y=f(x)为R上的增函数,g(x)=f-1(x),b=1,f(1)<1,证明对任意n∈N*,an+1<an(用t表示)。
(1)若f(x)≥tx+1,t≠0,t≠2,g(x)=2x,f(b)≠g(b),
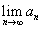 存在,求
存在,求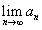 的值;
的值;(2)若函数y=f(x)为R上的增函数,g(x)=f-1(x),b=1,f(1)<1,证明对任意n∈N*,an+1<an(用t表示)。
解:(1)由题设知 得
得
又已知 ,可得
,可得
由 可知
可知
所以 是等比数列,其首项为
是等比数列,其首项为 ,公比为
,公比为 ,于是
,于是

即
又 存在,可得
存在,可得
所以-2<t<2且t≠0
∴ 。
。
(2)因为
所以
即
下面用数学归纳法证明an+1<an(n∈N*)
(i)当n=1时,由f(x)为增函数,且 <1,得
<1,得
 <1
<1
 <1
<1
 <
<
即a2<a1,结论成立
(ii)假设n=k时结论成立,即 <
< ,由f(x)为增函数,得
,由f(x)为增函数,得
f(ak+1)<f(ak),即 <
<
进而得 <f(
<f( )即
)即 <
<
这就是说当n=k+1时,结论也成立
根据(i)(ii)可知,对任意的n∈N*,an+1<an。
 得
得
又已知
 ,可得
,可得
由
 可知
可知
所以
 是等比数列,其首项为
是等比数列,其首项为 ,公比为
,公比为 ,于是
,于是
即

又
 存在,可得
存在,可得
所以-2<t<2且t≠0
∴
 。
。(2)因为

所以

即

下面用数学归纳法证明an+1<an(n∈N*)
(i)当n=1时,由f(x)为增函数,且
 <1,得
<1,得 <1
<1 <1
<1 <
<
即a2<a1,结论成立
(ii)假设n=k时结论成立,即
 <
< ,由f(x)为增函数,得
,由f(x)为增函数,得 f(ak+1)<f(ak),即
 <
<
进而得
 <f(
<f( )即
)即 <
<
这就是说当n=k+1时,结论也成立
根据(i)(ii)可知,对任意的n∈N*,an+1<an。

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目