Question

若函数f（x）=x²-2x+2，x∈[0，2]的值域为A，的定义域为B．
（1）求A和B；
（2）若A∩B=B，求实数a的取值范围．

Answer 1

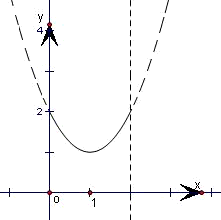解：（1）函数f（x）=x²-2x+2，x∈[0，2]的图象如图所示，
其值域为A=[1，2]；
由于-x²+（a+1）x-a≥0，得（x-1）（x-a）≤0，（*）
①若a=1，则（*）的解集为{1}，此时B={1}；
②若a＜1，则（*）的解集为[a，1]，此时B=[a，1]；
③若a＞1，则（*）的解集为[1，a]，此时B=[1，a]；
（2）要使A∩B=B，说明B是A的子集，
①若a=1，此时B={1}，符合题意；
②若a＜1，此时B=[a，1]，不合题意；
③若a＞1，此时B=[1，a]，需要a≤2，从而1＜a≤2
综上，故使A∩B=B的实数a的取值范围为1≤a≤2．
分析：（1）根据函数解析式有意义的原则可以求出集合B，根据二次函数在区间上的最值可以求出集合A；
（2）根据A∩B=B，说明B是A的子集，利用（1）中的结论，可构造关于a的不等式组，解不等式可得实数a的取值范围．
点评：本题考查的知识点是函数的定义域，函数的值域，集合的交集运算，其中求出集合A，B是解答的关键．