题目内容
已知数列{an}中,a1=2,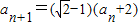 ,n=1,2,3,…
,n=1,2,3,…(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn}中,b1=2,
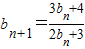 ,n=1,2,3,…,证明:
,n=1,2,3,…,证明: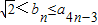 ,n=1,2,3,…
,n=1,2,3,…
【答案】分析:(Ⅰ)先对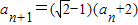 进行整理可得到
进行整理可得到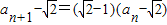 ,即数列
,即数列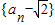 是首项为
是首项为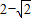 ,公比为
,公比为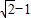 的等比数列,再由等比数列的通项公式可得到
的等比数列,再由等比数列的通项公式可得到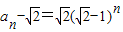 ,进而得到
,进而得到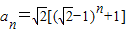 .
.
(Ⅱ)用数学归纳法证明.当n=1时可得到b1=a1=2满足条件,然后假设当n=k时满足条件进而得到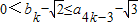 当n=k+1时再对
当n=k+1时再对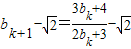 进行整理得到
进行整理得到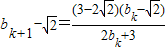
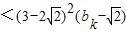
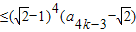 =
=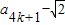 ,进而可得证.
,进而可得证.
解答:解:(Ⅰ)由题设: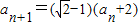 =
=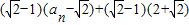 =
=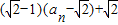 ,
,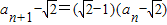 .
.
所以,数列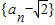 是首项为
是首项为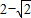 ,公比为
,公比为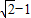 的等比数列,
的等比数列,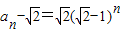 ,
,
即an的通项公式为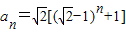 ,n=1,2,3,.
,n=1,2,3,.
(Ⅱ)用数学归纳法证明.
(ⅰ)当n=1时,因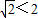 ,b1=a1=2,所以
,b1=a1=2,所以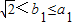 ,结论成立.
,结论成立.
(ⅱ)假设当n=k时,结论成立,即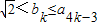 ,
,
也即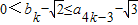 .
.
当n=k+1时,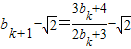 =
=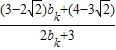 =
=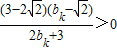 ,
,
又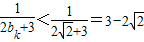 ,
,
所以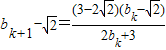
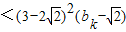
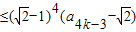 =
=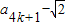 .
.
也就是说,当n=k+1时,结论成立.
根据(ⅰ)和(ⅱ)知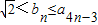 ,n=1,2,3,.
,n=1,2,3,.
点评:本题主要考查求数列的通项公式的方法--构造法和数学归纳法的一般过程.考查综合运用能力和计算能力.
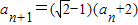 进行整理可得到
进行整理可得到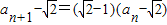 ,即数列
,即数列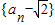 是首项为
是首项为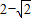 ,公比为
,公比为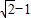 的等比数列,再由等比数列的通项公式可得到
的等比数列,再由等比数列的通项公式可得到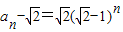 ,进而得到
,进而得到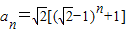 .
.(Ⅱ)用数学归纳法证明.当n=1时可得到b1=a1=2满足条件,然后假设当n=k时满足条件进而得到
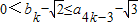 当n=k+1时再对
当n=k+1时再对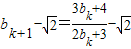 进行整理得到
进行整理得到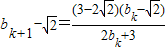
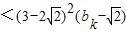
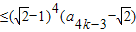 =
=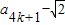 ,进而可得证.
,进而可得证.解答:解:(Ⅰ)由题设:
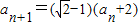 =
=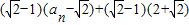 =
=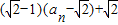 ,
,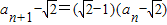 .
.所以,数列
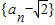 是首项为
是首项为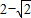 ,公比为
,公比为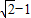 的等比数列,
的等比数列,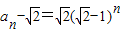 ,
,即an的通项公式为
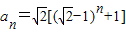 ,n=1,2,3,.
,n=1,2,3,.(Ⅱ)用数学归纳法证明.
(ⅰ)当n=1时,因
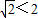 ,b1=a1=2,所以
,b1=a1=2,所以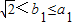 ,结论成立.
,结论成立.(ⅱ)假设当n=k时,结论成立,即
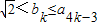 ,
,也即
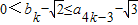 .
.当n=k+1时,
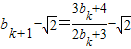 =
=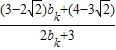 =
=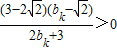 ,
,又
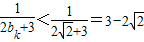 ,
,所以
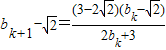
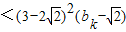
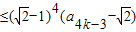 =
=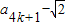 .
.也就是说,当n=k+1时,结论成立.
根据(ⅰ)和(ⅱ)知
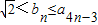 ,n=1,2,3,.
,n=1,2,3,.点评:本题主要考查求数列的通项公式的方法--构造法和数学归纳法的一般过程.考查综合运用能力和计算能力.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|