题目内容
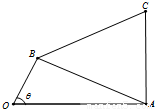
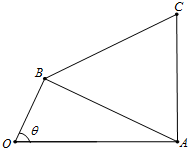 如图,四边形OACB中,a,b,c△ABC的内角A,B,C的对边,且满足sinB+sinC=2sin(B+C).
如图,四边形OACB中,a,b,c△ABC的内角A,B,C的对边,且满足sinB+sinC=2sin(B+C).(Ⅰ)证明:b+c=2a;
(Ⅱ)若b=c,设∠AOB=θ,(0<θ<π),OA=2OB=2,求四边形OACB面积的最大值.
分析:(Ⅰ)已知等式右边利用内角和定理及诱导公式变形,再利用正弦定理化简即可得证;
(Ⅱ)由b+c=2a,b=c,得到a=b=c,即三角形ABC为等边三角形,四边形ACBO面积=三角形AOB面积+三角形ABC面积,表示出四边形ACBO面积,利用正弦函数的值域即可确定出面积最大值.
(Ⅱ)由b+c=2a,b=c,得到a=b=c,即三角形ABC为等边三角形,四边形ACBO面积=三角形AOB面积+三角形ABC面积,表示出四边形ACBO面积,利用正弦函数的值域即可确定出面积最大值.
解答:(Ⅰ)证明:∵sin(B+C)=sinA,
∴sinB+sinC=2sinA,
利用正弦定理化简得:b+c=2a;
(Ⅱ)解:∵b+c=2a,b=c,
∴a=b=c,即△ABC为等边三角形,
∴S四边形OACB=S△OAB+S△ABC=
OA•OBsinθ+
AB2=sinθ+
(OA2+OB2-2OA•OBcosθ)=sinθ-
cosθ+
=2sin(θ-
)+
,
∵θ∈(0,π),
∴θ-
∈(-
,
),
当且仅当θ-
=
,即θ=
时取最大值,S四边形OACB的最大值为2+
.
∴sinB+sinC=2sinA,
利用正弦定理化简得:b+c=2a;
(Ⅱ)解:∵b+c=2a,b=c,
∴a=b=c,即△ABC为等边三角形,
∴S四边形OACB=S△OAB+S△ABC=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| 3 |
5
| ||
| 4 |
| π |
| 3 |
5
| ||
| 4 |
∵θ∈(0,π),
∴θ-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
当且仅当θ-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
5
| ||
| 4 |
点评:此题考查了正弦、余弦定理,三角形面积公式,以及正弦函数的值域,熟练掌握定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,目标函数z=ax-y的可行域为四边形OACB(含边界)若C(
如图所示,目标函数z=ax-y的可行域为四边形OACB(含边界)若C(| 2 |
| 3 |
| 4 |
| 5 |
A、(-
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|
 (2013•青岛一模)已知函数f(x)=sinωx(ω>0)在区间
(2013•青岛一模)已知函数f(x)=sinωx(ω>0)在区间 已知函数f(x)=sinωx(ω>0)在区间
已知函数f(x)=sinωx(ω>0)在区间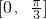 上单调递增,在区间
上单调递增,在区间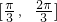 上单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足
上单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足 .
.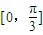 上单调递增,在区间
上单调递增,在区间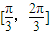 上单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足
上单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足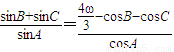 .
.