题目内容
若函数y=
是奇函数,则实数a的值为
| (x+1)(x+a) | x |
-1
-1
.分析:法一:由函数f(x)为奇函数,根据奇函数的性质得到f(-x)=-f(x),分别代入列出关于a的方程,即可求出a的值.
法二:由奇函数的性质可知,g(x)=(x+1)(x+a)=x2+(a+1)x+a为偶函数,根据偶函数的性质可知,函数的对称轴x=0可求a
法二:由奇函数的性质可知,g(x)=(x+1)(x+a)=x2+(a+1)x+a为偶函数,根据偶函数的性质可知,函数的对称轴x=0可求a
解答:解:由题意可得,x≠0,f(-x)=-f(x)
∴
=-
整理可得,2(a+1)x=0对任意x≠0都成立
∴a+1=0
∴a=-1
故答案为:-1
法二:∵y=
是奇函数
由奇函数的性质可知,g(x)=(x+1)(x+a)=x2+(a+1)x+a为偶函数
根据偶函数的性质可知,函数的对称轴x=-(a+1)=0
∴a=-1
故答案为:-1
∴
| (-x+1)(-x+a) |
| -x |
| (x+1)(x+a) |
| x |
整理可得,2(a+1)x=0对任意x≠0都成立
∴a+1=0
∴a=-1
故答案为:-1
法二:∵y=
| (x+1)(x+a) |
| x |
由奇函数的性质可知,g(x)=(x+1)(x+a)=x2+(a+1)x+a为偶函数
根据偶函数的性质可知,函数的对称轴x=-(a+1)=0
∴a=-1
故答案为:-1
点评:此题考查了函数奇偶性的性质,当函数为偶函数时有f(-x)=f(x);当函数为奇函数时有f(-x)=-f(x),熟练掌握此性质是解本题的关键

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
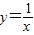 的定义域是{x|x>2},则它的值域是
的定义域是{x|x>2},则它的值域是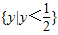 ;
;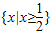 .
.