题目内容
某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题的便可提交通过.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力.
解:(Ⅰ)设考生甲、乙正确完成实验操作的题数分别为ξ、η,则ξ=1、2、3,η=0、1、2、3.
P(ξ=1)= =
= ,P(ξ=2)=
,P(ξ=2)= =
= ,P(ξ=3)=
,P(ξ=3)= =
= .
.
所以考生甲正确完成实验操作的题数的概率分布列为:
∴Eξ= =2.
=2.
∵η~B ,所以考生甲正确完成实验操作的题数的概率分布列为:
,所以考生甲正确完成实验操作的题数的概率分布列为:
P(η=k)= (k=0,1,2,3),
(k=0,1,2,3),
∴Eη=3× =2.
=2.
(Ⅱ)∵P(ξ≥2)= =
= ,P(η≥2)=
,P(η≥2)= .
.
∴P(ξ≥2)>P(η≥2),
从做对题的数学期望上甲乙两人水平相当;从至少完成两题的概率上看,甲通过的可能性比较大,因此可以判断甲的实验操作能力强.
分析:(Ⅰ)设考生甲、乙正确完成实验操作的题数分别为ξ、η,ξ服从超几何分布,η~B ,利用数学期望的计算公式即可得出;
,利用数学期望的计算公式即可得出;
(Ⅱ)分别从做对题的数学期望、从至少完成两题的概率上考查即可.
点评:熟练掌握超几何分别、二项分布、数学期望是解题的关键.
P(ξ=1)=
 =
= ,P(ξ=2)=
,P(ξ=2)= =
= ,P(ξ=3)=
,P(ξ=3)= =
= .
.
所以考生甲正确完成实验操作的题数的概率分布列为:
∴Eξ=
 =2.
=2.∵η~B
 ,所以考生甲正确完成实验操作的题数的概率分布列为:
,所以考生甲正确完成实验操作的题数的概率分布列为:P(η=k)=
 (k=0,1,2,3),
(k=0,1,2,3),∴Eη=3×
 =2.
=2.(Ⅱ)∵P(ξ≥2)=
 =
= ,P(η≥2)=
,P(η≥2)= .
.∴P(ξ≥2)>P(η≥2),
从做对题的数学期望上甲乙两人水平相当;从至少完成两题的概率上看,甲通过的可能性比较大,因此可以判断甲的实验操作能力强.
分析:(Ⅰ)设考生甲、乙正确完成实验操作的题数分别为ξ、η,ξ服从超几何分布,η~B
 ,利用数学期望的计算公式即可得出;
,利用数学期望的计算公式即可得出;(Ⅱ)分别从做对题的数学期望、从至少完成两题的概率上考查即可.
点评:熟练掌握超几何分别、二项分布、数学期望是解题的关键.

练习册系列答案
相关题目
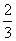 ,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力.
,且每题正确完成与否互不影响。试从至少正确完成2题的概率分析比较两位考生的实验操作能力. ,且每题正确完成与否互不影响。
,且每题正确完成与否互不影响。