题目内容
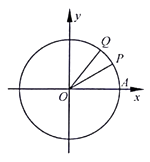
【题目】设A是单位圆O和x轴正半轴的交点，P，Q是圆O上两点，O为坐标原点，∠AOP= 
，∠AOQ=α，α∈[0， 
]． 
（1）若Q（ 
， 
），求cos（α﹣ ）的值；
（2）设函数f（α）=sinα（ 
），求f（α）的值域．
【答案】
（1）解：由已知得cosα= 
，sinα= 
，
∴cos（ 
）= 
+ × 
= 
（2）解： 
=（ 
， 
）， 
=（cosα，sinα），
∴ 
= 
cosα+ sinα，
∴f（α）= sinαcosα+ sin2α= 
sin2α﹣ 
cos2α+ = sin（2α﹣ 
）+ ．
∵α∈[0， 
]，∴2α﹣ ∈[﹣ ， 
]，
∴当2α﹣ =﹣ 时，f（α）取得最小值 
+ =0，
当2α﹣ = 时，f（α）取得最大值 
= 
．
∴f（α）的值域是[0， ]
【解析】（1）利用差角的余弦公式计算；（2）利用三角恒等变换化简f（α），再利用α的范围和正弦函数的性质求出f（α）的最值．
练习册系列答案
阅读快车系列答案
相关题目
【题目】假设某设备的使用年限x（年）和所支出的维修费用y（万元）有如下的统计资料：
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
试求：（1）y与x之间的回归方程；
（2）当使用年限为10年时，估计维修费用是多少？
