题目内容
12.某商场为回馈大客户,开展摸球中奖活动,规则如下:从一个装有质地和大小完全相同的4个白球和一个红球的摸奖箱中随机摸出一球,若摸出红球,则摸球结束,若摸出白球(不放回),则向摸奖箱中放入一个红球后继续进行下一轮摸球,直到摸出红球结束,若大客户在第n轮(n∈N*)摸到红球,则可获得$10000•{(\frac{1}{2})^{n-1}}$的奖金(单位:元)(Ⅰ)求某位大客户在一次摸球中奖活动中至少获得2500元奖金的概率;
(Ⅱ)设随机变量ξ为某位大客户所能获得的奖金,求随机变量ξ的概率分布列及数学期望.
分析 (Ⅰ)根据题意得出:ξ=$10000•{(\frac{1}{2})^{n-1}}$,确定ξ1=10000,ξ2=5000,ξ3=2500,ξ4=1250,ξ5=625,运公式求解概率P(ξ1=10000),P(ξ2=5000),P(ξ3=2500),
P(ξ4=1250),P(ξ5=625),运用加法得出至少获得2500元奖金的概率;
(Ⅱ)根据概率分列 求解即可,准确计算.
解答 解;客户摸的次数为1,2,3,4,5
(Ⅰ)根据题意得出:ξ=$10000•{(\frac{1}{2})^{n-1}}$
ξ1=10000,ξ2=5000,ξ3=2500,ξ4=1250,ξ5=625
P(ξ1=10000)=$\frac{1}{5}$;
P(ξ2=5000)=$\frac{4}{5}$×$\frac{2}{5}$=$\frac{8}{25}$;
P(ξ3=2500)=$\frac{4}{5}$×$\frac{3}{5}$×$\frac{3}{5}$=$\frac{36}{125}$;
P(ξ4=1250)=$\frac{4}{5}$×$\frac{3}{5}$×$\frac{2}{5}$×$\frac{4}{5}$=$\frac{96}{625}$;
P(ξ5=625)=$\frac{4}{5}$×$\frac{3}{5}$×$\frac{2}{5}$×$\frac{1}{5}$×1=$\frac{24}{625}$,
(Ⅱ)某位大客户在一次摸球中奖活动中至少获得2500元奖金的概率为:$\frac{1}{5}$$+\frac{8}{25}$$+\frac{36}{125}$=$\frac{101}{125}$
| ξ | 10000 | 5000 | 2500 | 1250 | 625 |
| P | $\frac{1}{5}$ | $\frac{8}{25}$ | $\frac{36}{125}$ | $\frac{96}{625}$ | $\frac{24}{625}$ |
点评 本题考查了古典概率问题在实际问题中的应用,关键是根据题意得出随机变量的值,运用独立事件同时发生的概率计算求解,属于中档题,计算数学期望要仔细认真.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| A. | 若直线l∥平面α,直线l∥平面β,则α∥β. | |
| B. | 若直线l⊥平面α,直线l⊥平面β,则α∥β. | |
| C. | 若直线l1,l2与平面α所成的角相等,则l1∥l2 | |
| D. | 若直线l上两个不同的点A,B到平面α的距离相等,则l∥α |
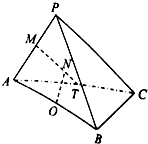 如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.
如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.