题目内容
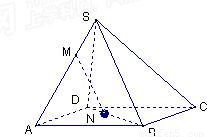
如图：S是平行四边形ABCD平面外一点，M，N分别是SA，BD上的点，且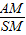
=
，求证：MN∥平面SBC．
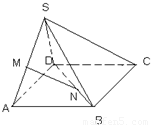
【答案】分析：在SD上取一点Q，使
=
=
，则有MQ∥AD，NQ∥SB．证得平面SBC∥平面MNQ，可得MN∥平面SBC．
解答：证明：在SD上取一点Q，使
=
=
，则有MQ∥AD，NQ∥SB．
再由ABCD为平行四边形，可得MQ∥BC．
由于MQ?平面MNQ，NQ?平面MNQ，SB、BC不在平面MNQ内，故SB∥平面MNQ，BC∥平面MNQ．
而SB BC是平面SBC内的两条相交直线，故有平面SBC∥平面MNQ．
而MN?平面MNQ，∴MN∥平面SBC．
点评：本题主要考查两个平面平行的性质，直线和平面平行的判定定理的应用，属于中档题．
==，则有MQ∥AD，NQ∥SB．证得平面SBC∥平面MNQ，可得MN∥平面SBC．解答：证明：在SD上取一点Q，使
==，则有MQ∥AD，NQ∥SB．再由ABCD为平行四边形，可得MQ∥BC．
由于MQ?平面MNQ，NQ?平面MNQ，SB、BC不在平面MNQ内，故SB∥平面MNQ，BC∥平面MNQ．
而SB BC是平面SBC内的两条相交直线，故有平面SBC∥平面MNQ．
而MN?平面MNQ，∴MN∥平面SBC．
点评：本题主要考查两个平面平行的性质，直线和平面平行的判定定理的应用，属于中档题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
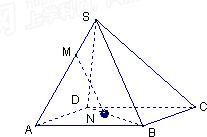
如图：S是平行四边形ABCD平面外一点，M，N分别是SA，BD上的点，且
=
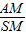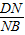，求证：MN∥平面SBC