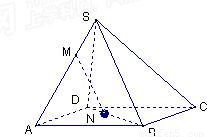
题目内容
如图：S是平行四边形ABCD平面外一点，M，N分别是SA，BD上的点，且| AM |
| SM |
| DN |
| NB |
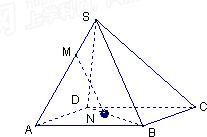
分析：在AB上取一点P，使
=
，则 MP∥SB，MP∥平面SBC．再证明NP∥平面SBC，得到平面MNP∥平面SBC，从而MN∥平面SBC．
| AP |
| BP |
| DN |
| NB |
解答：证明：在AB上取一点P，使
=
，则 MP∥SB．∵SB?面SBC，MP不在平面SBC内，
∴MP∥平面SBC． 又∵
=
，∴
=
，∴NP∥AD．
再由ABCD为平行四边形，∴NP∥BC，BC?面SBC，NP不在平面SBC内，∴NP∥平面SBC．
∴平面MNP∥平面SBC，而 MN?平面MNP∴MN∥平面SBC．
| AP |
| BP |
| AM |
| SM |
∴MP∥平面SBC． 又∵
| AM |
| SM |
| DN |
| NB |
| AP |
| BP |
| DN |
| NB |
再由ABCD为平行四边形，∴NP∥BC，BC?面SBC，NP不在平面SBC内，∴NP∥平面SBC．
∴平面MNP∥平面SBC，而 MN?平面MNP∴MN∥平面SBC．
点评：本题考查通过证明面面平行来来证明线面平行的方法，在AB上取一点P，使
=
，是解题的突破口．
| AP |
| BP |
| AM |
| SM |
练习册系列答案
名校课堂系列答案
相关题目
如图：S是平行四边形ABCD平面外一点，M，N分别是SA，BD上的点，且
=
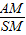，求证：MN∥平面SBC．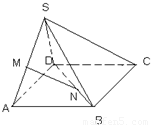
=
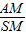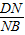，求证：MN∥平面SBC