Question

【题目】在平面直角坐标系xOy中，已知椭圆Γ： =1，A为Γ的上顶点，P为Γ上异于上、下顶点的动点，M为x正半轴上的动点．
（1）若P在第一象限，且|OP|= ，求P的坐标；
（2）设P（ ），若以A、P、M为顶点的三角形是直角三角形，求M的横坐标；
（3）若|MA|=|MP|，直线AQ与Γ交于另一点C，且 ， ，求直线AQ的方程．

Answer 1

【答案】
（1）解：设P（x，y）（x＞0，y＞0），

∵椭圆Γ： =1，A为Γ的上顶点，

P为Γ上异于上、下顶点的动点，

P在第一象限，且|OP|= ，

∴联立 ，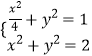

解得P（ ， ）

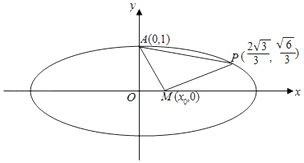
（2）解：设M（x0，0），A（0，1），

P（ ），

若∠P=90°，则 ，即（x0﹣ ，﹣ ）（﹣ ， ）=0，

∴（﹣ ）x0+ ﹣ =0，解得x0= ．

如图，若∠M=90°，则 =0，即（﹣x0，1）（ ﹣x0， ）=0，

∴ =0，解得x0=1或x0= ，

若∠A=90°，则M点在x轴负半轴，不合题意．

∴点M的横坐标为 ，或1，或

（3）解：设C（2cosα，sinα），

∵ ，A（0，1），

∴Q（4cosα，2sinα﹣1），

又设P（2cosβ，sinβ），M（x0，0），

∵|MA|=|MP|，∴x02+1=（2cosβ﹣x0）2+（sinβ）2，

整理得：x0= cosβ，

∵ =（4cosα﹣2cosβ，2sinα﹣sinβ﹣1）， =（﹣ cosβ，﹣sinβ）， ，

∴4cosα﹣2cosβ=﹣5cosβ，

且2sinα﹣sinβ﹣1=﹣4sinβ，

∴cosβ=﹣ cosα，且sinα= （1﹣2sinα），

以上两式平方相加，整理得3（sinα）2+sinα﹣2=0，∴sinα= ，或sinα=﹣1（舍去），

此时，直线AC的斜率kAC=﹣ = （负值已舍去），如图．

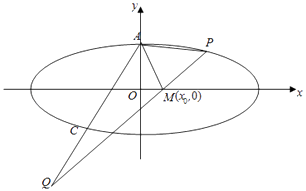
∴直线AQ为y= x+1．

【解析】（1）设P（x，y）（x＞0，y＞0），联立 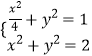，能求出P点坐标．（2）设M（x0，0），A（0，1），P（ ），由∠P=90°，求出x0= ；由∠M=90°，求出x0=1或x0= ；由∠A=90°，则M点在x轴负半轴，不合题意．由此能求出点M的横坐标．（3）设C（2cosα，sinα），推导出Q（4cosα，2sinα﹣1），设P（2cosβ，sinβ），M（x0，0）推导出x0= cosβ，从而 4cosα﹣2cosβ=﹣5cosβ，且2sinα﹣sinβ﹣1=﹣4sinβ，cosβ=﹣ cosα，且sinα= （1﹣2sinα），由此能求出直线AQ．