题目内容
在平面直角坐标系中,已知点P(1,-1),过点P作抛物线T0:y=x2的切线,其切点分别为M(x1,y1),N(x2,y2)(其中x1<x2).
(1)求x1与x2的值;
(2)若以点P为圆心的圆与直线MN相切,求圆的面积.
解:(1)由y=x2可得,y′=2x.
∵直线PM与曲线T0相切,且过点P(1,-1),
∴ ,即x12-2x1-1=0,
,即x12-2x1-1=0,
∴ ,或
,或 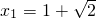 ,
,
同理可得: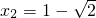 ,或
,或 
∵x1<x2,∴ ,
, .
.
(2)由(1)知,x1+x2=2,x1•x2=-1,
则直线MN的斜率 ,
,
∴直线M的方程为:y-y1=(x1+x2)(x-x1),又y1=x12,
∴y-x12=(x1+x2)x-x12-x1x2,即2x-y+1=0.
∵点P到直线MN的距离即为圆E的半径,即 ,
,
故圆E的面积为 .
.
分析:(1)由y=x2先求出y′=2x.再由直线PM与曲线T0相切,且过点P(1,-1),得到 ,或
,或 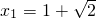 .同理可得
.同理可得 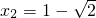 ,或
,或  ,然后由x1<x2知
,然后由x1<x2知  ,
, .
.
(2)由题意知,x1+x2=2,x1•x2=-1,则直线MN的方程为:2x-y+1=0.再由点P到直线MN的距离即为圆E的半径,从而可求出圆E的面积.
点评:本题以直线与抛物线的位置关系为载体,考查直线与抛物线相切,考查点线距离公式,解题的关键是合理运用导数求切线方程
∵直线PM与曲线T0相切,且过点P(1,-1),
∴
 ,即x12-2x1-1=0,
,即x12-2x1-1=0,∴
 ,或
,或 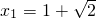 ,
,同理可得:
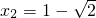 ,或
,或 
∵x1<x2,∴
 ,
, .
.(2)由(1)知,x1+x2=2,x1•x2=-1,
则直线MN的斜率
 ,
,∴直线M的方程为:y-y1=(x1+x2)(x-x1),又y1=x12,
∴y-x12=(x1+x2)x-x12-x1x2,即2x-y+1=0.
∵点P到直线MN的距离即为圆E的半径,即
 ,
,故圆E的面积为
 .
.分析:(1)由y=x2先求出y′=2x.再由直线PM与曲线T0相切,且过点P(1,-1),得到
 ,或
,或 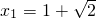 .同理可得
.同理可得 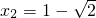 ,或
,或  ,然后由x1<x2知
,然后由x1<x2知  ,
, .
.(2)由题意知,x1+x2=2,x1•x2=-1,则直线MN的方程为:2x-y+1=0.再由点P到直线MN的距离即为圆E的半径,从而可求出圆E的面积.
点评:本题以直线与抛物线的位置关系为载体,考查直线与抛物线相切,考查点线距离公式,解题的关键是合理运用导数求切线方程

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目