题目内容
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是.

A.
| B.
| C.
| D.
|


如图,设D为BC中点,则 PD⊥BC,PD⊥MN,垂足为E,E为MN中点.又面AMN⊥面PBC,则 PE⊥面AMN,PE⊥AE.
设底面边长为2,侧棱长为a,在△PBC中,PD2=a2-1,PE2=
| 1 |
| 4 |
| a2-1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
在△PAB中,由余弦定理,cos∠APB=
| SA2+SB2-AB2 |
| 2SB×SA |
| SA2+SM2-AM2 |
| 2SM×SA |
| a2-2 |
| a2 |
| ||
| a2 |
| a2 |
| 4 |
在△PAE中,由勾股定理,得出 PA2=AE2+PE2=AM2-ME2+PE2,即a2=
| a2 |
| 4 |
| 1 |
| 4 |
| a2-1 |
| 4 |
| 3 |
设O为底面△ABC中心,连接OB,则∠PBO为三棱锥的侧棱PB与底面所成角,
在△POB中,BO=
2
| ||
| 3 |
| 5 |
| 3 |
| ||
| 3 |
| PO |
| BO |
| ||
| 2 |
三棱锥的侧棱与底面所成角的正切值是
| ||
| 2 |
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
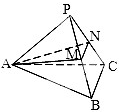 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,底面边长为2,则此三棱锥的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
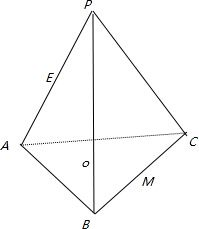 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP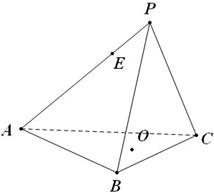 如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP
如图,在正三棱锥P-ABC中,点O为底面中心,点E在PA上,且AE=2EP 如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是.
如图,在正三棱锥P-ABC中,M、N分别是侧棱PB、PC的中点,若截面AMN⊥侧面PBC,则此三棱锥的侧棱与底面所成角的正切值是. 如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )
如图,在正三棱锥P-ABC中,M,N分别是侧棱PB、PC上的点,若PM:MB=CN:NP=2:1,且平面AMN⊥平面PBC,则二面角A-BC-P的平面角的余弦值为( )