题目内容
8.已知$sin(π+α)=\frac{1}{3}$,则cos2α=( )| A. | $\frac{7}{9}$ | B. | $\frac{8}{9}$ | C. | $-\frac{7}{9}$ | D. | $\frac{{4\sqrt{2}}}{9}$ |
分析 由已知及诱导公式可求sinα,由二倍角的余弦函数公式即可得解.
解答 解:∵$sin(π+α)=\frac{1}{3}$,∴可得sinα=-$\frac{1}{3}$,
∴cos2α=1-2sin2α=1-2×$\frac{1}{9}$=$\frac{7}{9}$.
故选:A.
点评 本题主要考查了诱导公式,二倍角的余弦函数公式的应用,属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
16.已知奇函数y=f(x)的导函数f′(x)<0在R恒成立,且x,y满足不等式f(x2-2x)+f(y2-2y)≥0,则$\sqrt{{x^2}+{y^2}}$的取值范围是( )
| A. | $[0,2\sqrt{2}]$ | B. | $[0,\sqrt{2}]$ | C. | [1,2] | D. | $[\sqrt{2},2\sqrt{2}]$ |
11.若关于x的方程ax-x-a=0有两个解,则实数a的取值范围是( )
| A. | (1,+∞) | B. | (0,1) | C. | (0,+∞) | D. | ∅ |
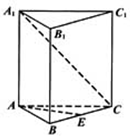 如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF
如图,已知正三棱柱ABC-A1B1C1的各棱长均相等,E是BC的中点,点F在侧棱CC1上,且CC1=4CF 某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测评,该班的A、B两个小组所有同学所得分数(百分制)的茎叶图如图所示,其中B组一同学的分数已被污损,但知道B组学生的平均分比A组学生的平均分高1分.
某校团委会组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名同学,在实践活动结束后,学校团委会对该班的所有同学都进行了测评,该班的A、B两个小组所有同学所得分数(百分制)的茎叶图如图所示,其中B组一同学的分数已被污损,但知道B组学生的平均分比A组学生的平均分高1分.