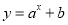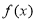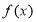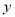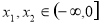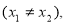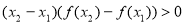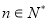题目内容
已知圆 .
.
(1)若圆 的切线在
的切线在 轴和
轴和 轴上的截距相等,且截距不为零,求此切线的方程;
轴上的截距相等,且截距不为零,求此切线的方程;
(2)从圆 外一点
外一点 向该圆引一条切线,切点为
向该圆引一条切线,切点为 ,
, 为坐标原点,且有
为坐标原点,且有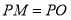 ,求使
,求使 的长取得最小值的点
的长取得最小值的点 的坐标.
的坐标.
(1)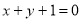 或
或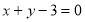 ;(2)
;(2)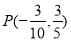 .
.
【解析】
试题分析:(1)根据题意可设切线方程为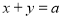 (
(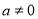 ),然后利用圆心到切线的距离等于半径即可求出
),然后利用圆心到切线的距离等于半径即可求出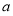 的值,进而求出切线方程;
的值,进而求出切线方程;
(2)通过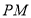 为切线,可知
为切线,可知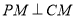 ,可以得到点
,可以得到点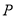 的轨迹方程,然后将求
的轨迹方程,然后将求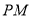 的最小值问题转化为求
的最小值问题转化为求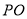 的最小值,利用点到直线的距离易得.
的最小值,利用点到直线的距离易得.
试题解析:(1) 切线在两坐标轴上的截距相等且截距不为零,
切线在两坐标轴上的截距相等且截距不为零,
∴设切线方程为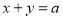 (
(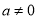 ),
),
又 圆C:
圆C: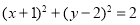 ,
,
∴圆心C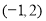 到切线的距离等于圆的半径
到切线的距离等于圆的半径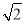 ,
,
∴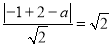 ,解得
,解得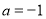 或
或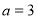 ,
,
故所求切线的方程为: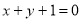 或
或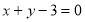 .
.
(2)设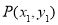 ,
,
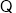 切线
切线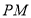 与半径
与半径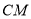 垂直,
垂直,
∴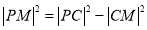 ,
,
∴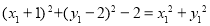 ,整理得
,整理得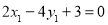 ,
,
故动点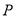 在直线
在直线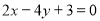 上,
上,
由已知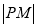 的最小值就是
的最小值就是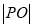 的最小值,
的最小值,
而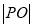 的最小值为
的最小值为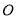 到直线
到直线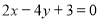 的距离
的距离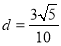 ,
,
∴ 解得
解得
∴所求点坐标为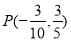 .
.
考点:1.直线与圆的位置关系;2.圆的切线问题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目