题目内容
17.已知cosα=-$\frac{15}{17}$,α∈($π,\frac{3}{2}π$),求sin2α,cos$\frac{α}{2}$的值.分析 由同角三角函数基本关系和角的范围可得sinα,由二倍角正弦可得sin2α,又可得cos$\frac{α}{2}$<0,由半角公式可得.
解答 解:∵cosα=-$\frac{15}{17}$,α∈($π,\frac{3}{2}π$),
∴sinα=-$\sqrt{1-co{s}^{2}α}$=-$\frac{8}{17}$,
∴sin2α=2sinαcosα=$\frac{240}{289}$;
由α∈($π,\frac{3}{2}π$)可得$\frac{α}{2}$∈($\frac{π}{2}$,$\frac{3π}{4}$),
∴cos$\frac{α}{2}$<0,
再由cosα=2cos2$\frac{α}{2}$-1=-$\frac{15}{17}$可解得cos$\frac{α}{2}$=$\frac{\sqrt{17}}{17}$
点评 本题考查倍角公式和半角公式,注意角的范围影响函数值的正负是解决问题的关键,属基础题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
12.据市场调查结果,预测某种家用商品从2014年初开始,n个月内累计的需求量Sn(万件)近似地满足Sn=2ln2-n3(n=1,2,…,12),按此预测在本年度内,需求量最大的月份是( )
| A. | 5月、6月 | B. | 6月、7月 | C. | 7月、8月 | D. | 8月、9月 |
1.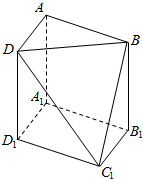 在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )
在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )
 在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )
在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{3}$ | D. | $\frac{5}{2}$ |
 如图,已知平面直角坐标系中点Q(2,0)和圆O:x2+y2=1,动点M到圆O的切线长|MN|与|MQ|相等,求动点M的轨迹方程.
如图,已知平面直角坐标系中点Q(2,0)和圆O:x2+y2=1,动点M到圆O的切线长|MN|与|MQ|相等,求动点M的轨迹方程.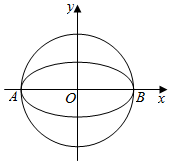 如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.