题目内容
求值
(1)已知向量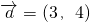 ,
, 且
且 ∥
∥ ,则
,则 的值
的值
(2)已知 ,则tan(α+β)的值.
,则tan(α+β)的值.
解:(1)∵向量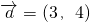 ,
, 且
且 ∥
∥ ,
,
∴ ,
,
∴ ,
,
∴ =
=
=
=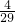 .
.
(2)∵ ,
,
∴tan(α+β)
=
=
=
=1.
分析:(1)由向量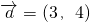 ,
, 且
且 ∥
∥ ,知
,知 ,把
,把 分子分母同时除以cosα,得到
分子分母同时除以cosα,得到 ,由此能求出结果.
,由此能求出结果.
(2)由 ,和tan(α+β)=
,和tan(α+β)= ,利用正切加法定理能够求出tan(α+β)的值.
,利用正切加法定理能够求出tan(α+β)的值.
点评:第(1)题考查平面向量平行的性质的应用,是基础题.解题时要认真审题,注意同角三角函数的性质的灵活运用.
第(2)题考查正切加法定理的应用,是基础题.解题时要认真审题,仔细解答.
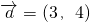 ,
, 且
且 ∥
∥ ,
,∴
 ,
,∴
 ,
,∴
 =
=
=

=
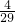 .
.(2)∵
 ,
,∴tan(α+β)
=

=

=

=1.
分析:(1)由向量
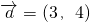 ,
, 且
且 ∥
∥ ,知
,知 ,把
,把 分子分母同时除以cosα,得到
分子分母同时除以cosα,得到 ,由此能求出结果.
,由此能求出结果.(2)由
 ,和tan(α+β)=
,和tan(α+β)= ,利用正切加法定理能够求出tan(α+β)的值.
,利用正切加法定理能够求出tan(α+β)的值.点评:第(1)题考查平面向量平行的性质的应用,是基础题.解题时要认真审题,注意同角三角函数的性质的灵活运用.
第(2)题考查正切加法定理的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 ,
, 且
且 ∥
∥ ,则
,则 的值
的值 ,则tan(α+β)的值.
,则tan(α+β)的值.