题目内容
在焦点在x轴的椭圆过点P（3，0），且长轴长是短轴长的3倍，则其标准方程为
+y2=1
+y2=1．
| x2 |
| 9 |
| x2 |
| 9 |
分析：设椭圆的方程为
+
=1（a＞b＞0），根据题意建立关于a、b的等式，解出a、b之值，可得该椭圆的标准方程．
| x2 |
| a2 |
| y2 |
| b2 |
解答：解：∵椭圆的焦点在x轴上，
∴可设椭圆的方程为
+
=1（a＞b＞0）．
又∵椭圆过点P（3，0），且长轴长是短轴长的3倍，
∴a=3且2a=3×2b，可得b=1
因此，该椭圆的标准方程为
+y2=1．
故答案为：
+y2=1
∴可设椭圆的方程为
| x2 |
| a2 |
| y2 |
| b2 |
又∵椭圆过点P（3，0），且长轴长是短轴长的3倍，
∴a=3且2a=3×2b，可得b=1
因此，该椭圆的标准方程为
| x2 |
| 9 |
故答案为：
| x2 |
| 9 |
点评：本题给出满足条件的椭圆，求椭圆的标方程．着重考查了椭圆的标准方程与简单几何性质等知识，属于基础题．
练习册系列答案
全能练考卷系列答案
相关题目
，且过点（
，
）. 
：
（
）与椭圆E交于
、
两点，证明直线
与直线
的交点在垂直于
轴的定直线上，并求出该直线方程．
．
·
＞－
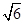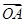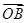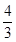，求k的取值范围．