题目内容
【题目】已知左、右焦点分别为![]() 的椭圆
的椭圆![]() 过点
过点![]() ,且椭圆C关于直线x=c对称的图形过坐标原点.
,且椭圆C关于直线x=c对称的图形过坐标原点.
(I)求椭圆C的离心率和标准方程。
(II)圆![]() 与椭圆C交于A,B两点,R为线段AB上任一点,直线
与椭圆C交于A,B两点,R为线段AB上任一点,直线![]() 交椭圆C于P,Q两点,若AB为圆
交椭圆C于P,Q两点,若AB为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于1,求
的斜率大于1,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】
(Ⅰ)利用椭圆C过点![]() ,∵椭圆C关于直线x=c对称的图形过坐标原点,推出a=2c,然后求解椭圆C的离心率,标准方程.
,∵椭圆C关于直线x=c对称的图形过坐标原点,推出a=2c,然后求解椭圆C的离心率,标准方程.
(Ⅱ)设A(![]() ),B(
),B(![]() ),利用中点坐标公式以及平方差法求出AB的斜率,得到直线AB的方程,代入椭圆C的方程求出点的坐标,设F1R:y=k(x+1),联立
),利用中点坐标公式以及平方差法求出AB的斜率,得到直线AB的方程,代入椭圆C的方程求出点的坐标,设F1R:y=k(x+1),联立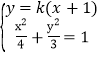 ,设P(x3,y3),Q(x4,y4),利用韦达定理,结合
,设P(x3,y3),Q(x4,y4),利用韦达定理,结合![]() ,
,![]() ,化简|PF1||QF1|,通过
,化简|PF1||QF1|,通过![]() ,求解|PF1||QF1|的取值范围.
,求解|PF1||QF1|的取值范围.
(Ⅰ)∵椭圆![]() 过点
过点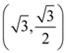 ,∴
,∴![]() ,①
,①
∵椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点,∴
对称的图形过坐标原点,∴![]() ,
,
∵![]() ,∴
,∴![]() ,②
,②
由①②得![]() ,
,![]() ,
,
∴椭圆![]() 的离心率
的离心率![]() ,标准方程为
,标准方程为![]() .
.
(Ⅱ)因为![]() 为圆
为圆![]() 的直径,所以点
的直径,所以点![]()
![]() 为线段
为线段![]() 的中点,
的中点,
设![]() ,
,![]() ,则,
,则,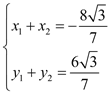 ,又
,又 ,
,
所以![]() ,则
,则![]() ,故
,故![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,即
,即![]() .代入椭圆
.代入椭圆![]() 的方程并整理得
的方程并整理得![]() ,
,
则![]() ,故直线
,故直线![]() 的斜率
的斜率![]() .
.
设![]() ,由
,由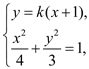 ,得
,得![]() ,
,
设![]() ,
,![]() ,则有
,则有![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
所以![]()
![]() =
=![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目