题目内容
已知函数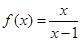 .
.
(Ⅰ)求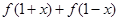 的值;
的值;
(Ⅱ)用函数单调性的定义证明函数 在
在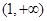 上是减函数.
上是减函数.
(Ⅰ)2;(Ⅱ)略
解析试题分析:(Ⅰ)将 整体代入原函数即可求
整体代入原函数即可求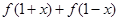 的值。(Ⅱ)在
的值。(Ⅱ)在 上任取两个实数,并规定其大小关系,如令
上任取两个实数,并规定其大小关系,如令 ,再用作差法比较
,再用作差法比较 的大小。最后利用函数单调性的定义得
的大小。最后利用函数单调性的定义得 在
在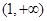 上的单调性。
上的单调性。
试题解析:(Ⅰ)解: 2分
2分 . 4分
. 4分
(Ⅱ)证明:设 是
是 上的两个任意实数,且
上的两个任意实数,且 ,
,  5分
5分 . 7分
. 7分
因为 ,所以
,所以 ,
, ,
, .所以
.所以 .
.
所以 . 9分
. 9分
所以 在
在 上是减函数. 10分
上是减函数. 10分
考点:求原函数值及函数单调性的定义。

练习册系列答案
相关题目
 x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)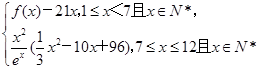
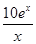 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)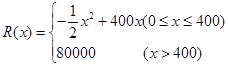 ,其中
,其中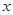 是组合床柜的月产量.
是组合床柜的月产量. 元表示为月产量
元表示为月产量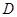 (分贝)由公式
(分贝)由公式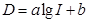 (
(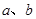 为非零常数)给出,其中
为非零常数)给出,其中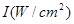 为声音能量.
为声音能量.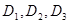 满足
满足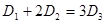 时,求对应的声音能量
时,求对应的声音能量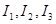 满足的等量关系式;
满足的等量关系式; 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为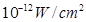 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪. ,其中
,其中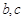 为常数.
为常数.  在区间
在区间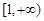 上单调,求
上单调,求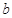 的取值范围;
的取值范围;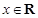 ,都有
,都有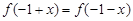 成立,且函数
成立,且函数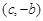 ,
,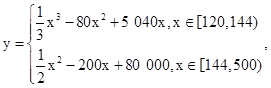
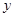 (单位:千套)与销售价格
(单位:千套)与销售价格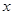 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式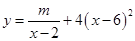 ,其中
,其中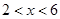 ,
,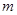 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.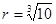 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.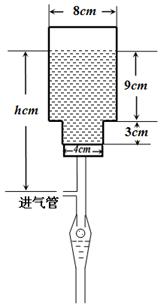
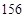 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?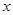 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为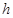 (单位:厘米),已知当
(单位:厘米),已知当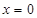 时,
时,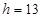 .试将
.试将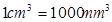 )
) 的定义域为
的定义域为 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:①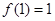 ;②对任意的
;②对任意的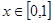 ,都有
,都有 ;③当
;③当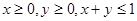 时总有
时总有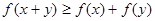 .
.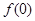 的值;
的值;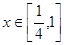 时,恒有
时,恒有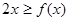 .
.