题目内容
【题目】在平面直角坐标系![]() 中,
中, ![]() 是抛物线
是抛物线![]() 的焦点,
的焦点, ![]() 是抛物线
是抛物线![]() 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过![]() 三点的圆的圆心为
三点的圆的圆心为![]() ,点
,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]()
(1)求抛物线![]() 的方程;
的方程;
(2)若点![]() 的横坐标为
的横坐标为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]()
![]() 与圆
与圆![]() 有两个不同的交点
有两个不同的交点![]() ,求当
,求当![]() 时,
时, ![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由圆的性质可得Q点纵坐标![]() ,根据抛物线定义可得
,根据抛物线定义可得![]() 即得抛物线方程(2)联立直线方程与抛物线方程。利用韦达定理及弦长公式可得
即得抛物线方程(2)联立直线方程与抛物线方程。利用韦达定理及弦长公式可得![]() ,利用垂径定理可得
,利用垂径定理可得![]() ,这样得到关于k的函数关系式,最后利用导数求其最值。
,这样得到关于k的函数关系式,最后利用导数求其最值。
试题解析:(1)F抛物线C:x2=2py(p>0)的焦点F![]() ,
,
设M![]() ,
,![]() ,由题意可知
,由题意可知![]() ,
,
则点Q到抛物线C的准线的距离为![]()
![]() ,解得
,解得![]() ,
,
于是抛物线C的方程为![]() 。
。
(Ⅲ)若点M的横坐标为![]() ,则点M
,则点M![]() ,
,![]() 。
。
由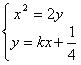 可得
可得![]() ,
,
设![]() ,
,![]()
![]()
圆![]() ,
,
![]() ,
,
于是![]() ,
,
令![]()
![]() ,
,
设![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
即当![]() 时
时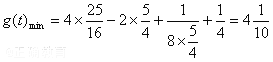 .
.
故当![]() 时,
时,![]() 。
。

【题目】某校随机调查80名学生,以研究学生爱好羽毛球运动与性别的关系,得到下面的![]() 列联表:
列联表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(Ⅰ)将此样本的频率视为总体的概率,随机调查本校的3名学生,设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)根据表3中数据,能否认为爱好羽毛球运动与性别有关?
| 0.050 | 0.010 |
| 3.841 | 6.635 |
附: ![]()
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.