题目内容
要使直线y=kx+1（k∈R）与焦点在x轴上的椭圆
+
=1总有公共点，实数a的取值范围是______．
| x2 |
| 7 |
| y2 |
| a |
要使方程
+
=1表示焦点在x轴上的椭圆，需a＜7，
由直线y=kx+1（k∈R）恒过定点（0，1），
所以要使直线y=kx+1（k∈R）与椭圆
+
=1总有公共点，
则（0，1）应在椭圆上或其内部，即a＞1，
所以实数a的取值范围是[1，7）．
故答案为[1，7）．
| x2 |
| 7 |
| y2 |
| a |
由直线y=kx+1（k∈R）恒过定点（0，1），
所以要使直线y=kx+1（k∈R）与椭圆
| x2 |
| 7 |
| y2 |
| a |
则（0，1）应在椭圆上或其内部，即a＞1，
所以实数a的取值范围是[1，7）．
故答案为[1，7）．
练习册系列答案
提分百分百检测卷系列答案
相关题目
要使直线y=kx+1（k∈R）与焦点在x轴上的椭圆
+
=1总有公共点，实数a的取值范围是（ ）
| x2 |
| 7 |
| y2 |
| a |
| A、0＜a≤1 |
| B、0＜a＜7 |
| C、1≤a＜7 |
| D、1＜a≤7 |
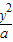=1总有公共点，则实数a的取值范围是（ ）
C.1≤a＜
D.1＜a≤
+
=1总有公共点，实数a的取值范围是（ ）
+
=1总有公共点，实数a的取值范围是（ ）