题目内容
已知抛物线C1：y2=x+7，圆C2：x2+y2=5．
（1）求证抛物线与圆没有公共点；
（2）过点P（a，0）作与x轴不垂直的直线l交C1，C2依次为A、B、C、D，若|AB|=|CD|，求实数a的变化范围．
解：（1）由
得x2+x+2=0，
∵△=1-8=-7＜0，
∴抛物线与圆没有公共点．
（2）由题意知AD与BC的中点相同，设l为y=k（x-a），
由
，得ky2-y-（7+a）k=0，
则
，
∴
，
由
得（1+k2）x2-2ak2x+a2k2-5=0，
则
，
∴
，∴
，
代入上述△中得-10
．
分析：（1）由得x2+x+2=0，由△=-7＜0，知抛物线与圆没有公共点．
（2）由题意知AD与BC的中点相同，设l为y=k（x-a），由，得ky2-y-（7+a）k=0，则，，由得（1+k2）x2-2ak2x+a2k2-5=0，由此可求出实数a的变化范围．
点评：本题考查直线和圆锥曲线的位置关系，解题时要认真审题，仔细解答．
得x2+x+2=0，∵△=1-8=-7＜0，
∴抛物线与圆没有公共点．
（2）由题意知AD与BC的中点相同，设l为y=k（x-a），
由
，得ky2-y-（7+a）k=0，则
，∴
，由
得（1+k2）x2-2ak2x+a2k2-5=0，则
，∴
，∴，代入上述△中得-10
．分析：（1）由
得x2+x+2=0，由△=-7＜0，知抛物线与圆没有公共点．（2）由题意知AD与BC的中点相同，设l为y=k（x-a），由
，得ky2-y-（7+a）k=0，则，，由得（1+k2）x2-2ak2x+a2k2-5=0，由此可求出实数a的变化范围．点评：本题考查直线和圆锥曲线的位置关系，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
（2012•河北模拟）已知抛物线C1：y2=2px和圆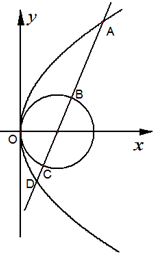
已知抛物线C1：y2=4x，圆C2：（x-1）2+y2=1，过抛物线焦点F的直线l交C1于A，D两点（点A在x轴上方），直线l交C2于B，C两点（点B在x轴上方）．