题目内容
在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成角为60°,E为PC的中点,则异面直线PA与BE所成角为( )
A.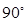 | B.  | C.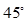 | D. |
C
解析试题分析:连接 交于点
交于点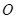 ,连接
,连接 ,
, 。因为
。因为 为
为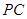 中点,所以
中点,所以 ∥
∥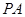 ,所以
,所以 即为异面直线
即为异面直线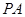 与
与 所成的角。因为四棱锥
所成的角。因为四棱锥 为正四棱锥,所以
为正四棱锥,所以 ,所以
,所以 为
为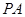 在面
在面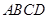 内的射影,所以
内的射影,所以 即为
即为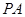 与面
与面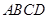 所成的角,即
所成的角,即 ,因为
,因为 ,所以
,所以 ,
, 。所以在直角三角形
。所以在直角三角形 中
中 ,即面直线
,即面直线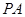 与
与 所成的角为
所成的角为 。
。
考点:1异面直线所成角;2线面角;3线面垂直。

练习册系列答案
相关题目
在空间中,有下列命题:①平行于同一直线的两条直线平行;②平行于同一直线的两个平面平行;③垂直于同一平面的两个平面平行;④垂直于同一平面的两条直线平行。
其中正确的命题个数有( )
| A.1 | B.2 | C.3 | D.4 |
点B是点A(1,2,3)在坐标平面 内的射影,则OB等于( )
内的射影,则OB等于( )
A. | B. | C. | D. |
已知直线 ⊥平面
⊥平面 ,直线m
,直线m ,给出下列命题:
,给出下列命题:
① ∥
∥ ②
② ∥m; ③
∥m; ③ ∥m
∥m ④
④ ∥
∥ 其中正确的命题是( )
其中正确的命题是( )
| A.①②③ | B.②③④ | C.②④ | D.①③ |
设 是一条直线,
是一条直线, ,
, ,
, 是不同的平面,则下列说法不正确的是( )
是不同的平面,则下列说法不正确的是( )
A.如果 ,那么 ,那么 内一定存在直线平行于 内一定存在直线平行于 |
B.如果 不垂直于 不垂直于 ,那么 ,那么 内一定不存在直线垂直于 内一定不存在直线垂直于 |
C.如果 , , , , ,那么 ,那么 |
D.如果 , , 与 与 , , 都相交,那么 都相交,那么 与 与 , , 所成的角互余 所成的角互余 |
已知两条不同的直线 ,两个不同的平面
,两个不同的平面 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.若 则 则 | B.若 则 则 |
C.若 则 则 | D.若 则 则 |
a,b,c是三条直线,α,β是两个平面,b?α,c?α,则下列命题不成立的是( )
| A.若α∥β,c⊥α,则c⊥β |
| B.“若b⊥β,则α⊥β”的逆命题 |
| C.若a是c在α内的射影,a⊥b,则b⊥c |
| D.“若b∥c,则c∥α”的逆否命题 |
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( ).
| A.若α⊥β,m?α,n?β,则m⊥n |
| B.若α∥β,m?α,n?β,,则m∥n |
| C.若m⊥n,m?α,n?β,则α⊥β |
| D.若m⊥α,m∥n,n∥β,则α⊥β |