Question

【题目】如图，直角三角形ABC的顶点坐标A（﹣2，0），直角顶点B（0，﹣2 ），顶点C在x轴上，点P为线段OA的中点，三角形ABC外接圆的圆心为M．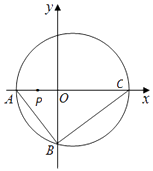

（1）求BC边所在直线方程；
（2）求圆M的方程；
（3）直线l过点P且倾斜角为 ，求该直线被圆M截得的弦长．

Answer 1

【答案】
（1）解：∵kAB=﹣ ，AB⊥BC

∴kBC= ，

∴BC边所在直线方程y= x﹣2 ．

（2）解：在上式中，令y=0得：C（4，0）…5分

∴圆心M（1，0）

又∵AM=3

∴外接圆的方程为（x﹣1）2+y2=9

（3）解：∵P（﹣1，0），直线l过点P且倾斜角为 ，∴直线l的方程为y= （x+1）…10分

点M到直线l的距离为

直线l被圆M截得的弦长为2 ．

【解析】（1）求出BC的斜率，可得BC边所在直线方程；（2）求出圆心与半径，即可求圆M的方程；（3）直线l过点P且倾斜角为 ，得出直线方程，即可求该直线被圆M截得的弦长．