题目内容
已知函数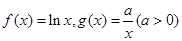 ,设
,设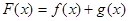
(1)求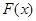 的单调区间;
的单调区间;
(2)若以 图象上任意一点
图象上任意一点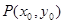 为切点的切线的斜率
为切点的切线的斜率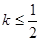 恒成立,求实数
恒成立,求实数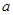 的最小值;
的最小值;
(3)是否存在实数 ,使得函数
,使得函数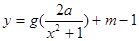 的图象与
的图象与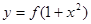 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
(1)增区间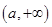 减区间
减区间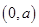 (2)
(2)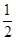 (3)
(3)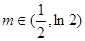
解析试题分析:(1)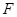
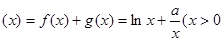 )
)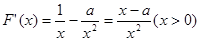
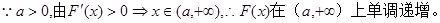
由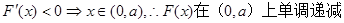 。
。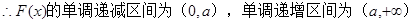
(2)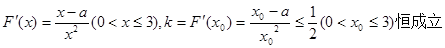
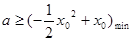 当
当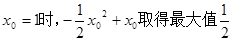
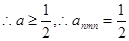
(3)若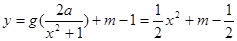 的图象与
的图象与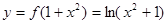 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即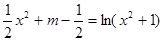 有四个不同的根,亦即
有四个不同的根,亦即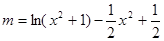 有四个不同的根。
有四个不同的根。
令 ,
,
则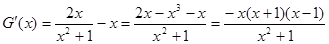 。
。
当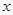 变化时
变化时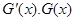 的变化情况如下表:
的变化情况如下表:
由表格知: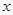
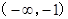
(-1,0) (0,1) (1,  )
)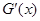 的符号
的符号+ - + - 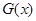 的单调性
的单调性↗ ↘ ↗ ↘  。
。
画出草图和验证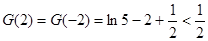 可知,当
可知,当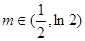 时,
时,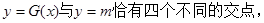

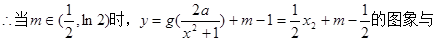
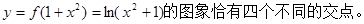
考点:函数单调性最值
点评:第二问第三问中的不等式恒成立或方程的根的问题都可通常转化为函数最值问题,这两种转化是常考知识点,须加以重视

练习册系列答案
相关题目
 的定义域为
的定义域为 ,且满足对于定义域内任意的
,且满足对于定义域内任意的 都有等式
都有等式 .
. 的值;
的值; ,且
,且 上是增函数,解关于
上是增函数,解关于 的不等式
的不等式 .
.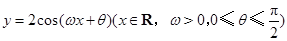 的图象与
的图象与 轴相交于点
轴相交于点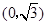 ,且该函数的最小正周期为
,且该函数的最小正周期为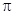 .
.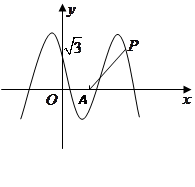
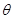 和
和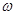 的值;
的值;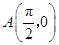 ,点
,点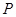 是该函数图象上一点,
是该函数图象上一点,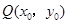 是
是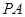 的中点,当
的中点,当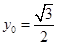 ,
,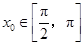 时,求
时,求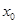 的值.
的值.  上有意义的两个函数
上有意义的两个函数 如果有任意
如果有任意
 则称
则称 与
与 在
在 与
与 给定区间
给定区间 , 讨论
, 讨论 与
与 在给定区间
在给定区间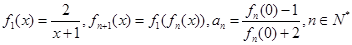
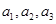 ,并求数列
,并求数列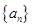 的通项公式.
的通项公式. 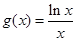 在
在 上为减函数,设数列
上为减函数,设数列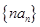 的前
的前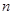 的和为
的和为 ,
,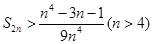
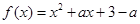 ,其中
,其中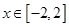 。
。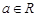 时,讨论它的单调性;
时,讨论它的单调性;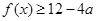 恒成立,求
恒成立,求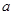 的取值范围.
的取值范围. (a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1="3," x2=4.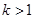 ,解关于x的不等式;
,解关于x的不等式;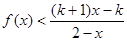 .
. ,当
,当 时函数
时函数 取得一个极值,其中
取得一个极值,其中 .
. 与
与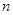 的关系式;
的关系式; 时,函数
时,函数 的图象上任意一点的切线的斜率恒大于
的图象上任意一点的切线的斜率恒大于 ,求
,求