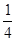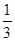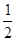题目内容
设 ,
, ,
, 是空间任意的非零向量,且相互不共线,则以下命题中:
是空间任意的非零向量,且相互不共线,则以下命题中:
①( ·
· )·
)· -(
-( ·
· )·
)· =0;②
=0;② ;③若存在唯一实数组
;③若存在唯一实数组 使
使 ,则
,则 ,
, ,
, 共面;④
共面;④ .
.
真命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:对于①, ,
, 是不共线的两个非零向量,又
是不共线的两个非零向量,又 ·
· 与
与 ·
· 均不为零,所以①假命题;对于②,因为三角形两边之和大于第三边,所以②是真命题;对于③,当实数组
均不为零,所以①假命题;对于②,因为三角形两边之和大于第三边,所以②是真命题;对于③,当实数组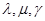 全为零时,则
全为零时,则 ,
, ,
, 可能不共面,所以③是假命题;对于④是假命题.故选B.
可能不共面,所以③是假命题;对于④是假命题.故选B.
考点:1.向量共线的基本定理;2.数乘向量的运算;3.向量数量积的几何意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数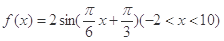 的图象与x轴交于点
的图象与x轴交于点 ,过点
,过点 的直线
的直线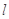 与函数
与函数 的图象交于
的图象交于 两点,则
两点,则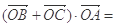 ( )
( )
A.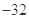 | B.16 | C.32 | D.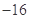 |
已知向量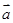 、
、 满足
满足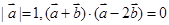 ,则
,则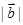 的取值范围为( )
的取值范围为( )
A. | B.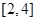 | C.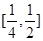 | D.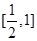 |
已知| |=3,|
|=3,| |=5,且
|=5,且 ,则向量
,则向量 在向量
在向量 上的投影为( )
上的投影为( )
A. | B.3 | C.4 | D.5 |
已知向量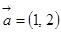 ,
,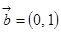 ,
,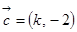 ,若(
,若(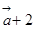
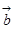 )
)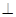
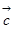 ,则
,则 ( )
( )
| A.2 | B.-2 | C.8 | D.-8 |
已知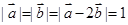 ,则
,则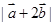 =( )
=( )
| A.9 | B.3 | C.1 | D.2 |
已知向量 ,若
,若 与
与 共线,则x的值为( )
共线,则x的值为( )
| A. 4 | B. 8 | C. 0 | D.2 |
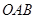 中,点
中,点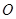 为原点,点
为原点,点 的坐标是
的坐标是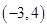 ,点
,点 在第一象限,向量
在第一象限,向量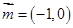 ,记向量
,记向量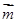 与向量
与向量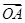 的夹角为
的夹角为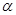 ,则
,则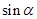 的值为( )
的值为( )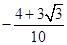
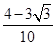
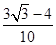
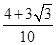
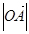 =1,
=1,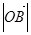 =
=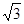 ,
,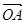 ·
·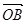 =0,点C在∠AOB内,且∠AOC=60°,设
=0,点C在∠AOB内,且∠AOC=60°,设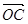 =m
=m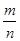 =( )
=( )