题目内容
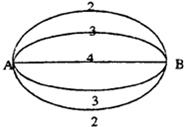 如图,A、B两点有5条连线并联,它们在单位时间内通过的信息量依次为2,3,4,3,2.现在任取三条线且记在单位时间内通过的信息总量为ξ.
如图,A、B两点有5条连线并联,它们在单位时间内通过的信息量依次为2,3,4,3,2.现在任取三条线且记在单位时间内通过的信息总量为ξ.(Ⅰ)写出信息总量ξ的分布列;
(Ⅱ)求信息总量ξ的数学期望.
分析:(Ⅰ)由题意知单位时间内通过的信息总量为ξ的取值2+2+3=7,2+3+3=8,2+3+4=9,3+3+4=10,结合变量对应的事件得到四个事件的概率,写出分布列和.
(1)根据上一问做出的分布列,求出期望,这种题目一般出现在一问里,不会分开来解.
(1)根据上一问做出的分布列,求出期望,这种题目一般出现在一问里,不会分开来解.
解答:解:(Ⅰ)由题意知单位时间内通过的信息总量为ξ的取值为7,8,9,10,
结合变量对应的事件得到
∵P(ξ=7)=
=
,P(ξ=8)=
=
,
P(ξ=9)=
=
,P(ξ=10)=
=
∴ξ的分布列为:

(Ⅱ)E(ξ)=
×7+
×8+
×9+
×10
=
=8.4
结合变量对应的事件得到
∵P(ξ=7)=
| ||||
|
| 1 |
| 5 |
| ||||||||
|
| 3 |
| 10 |
P(ξ=9)=
| ||||||
|
| 2 |
| 5 |
| ||||
|
| 1 |
| 10 |
∴ξ的分布列为:

(Ⅱ)E(ξ)=
| 1 |
| 5 |
| 3 |
| 10 |
| 2 |
| 5 |
| 1 |
| 10 |
=
| 42 |
| 5 |
点评:这道题出的有点与众不同,它是一个求概率和期望的问题,但是可以一气呵成的问题分成了两部分,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,只要注意解题格式就问题不大.

练习册系列答案
相关题目
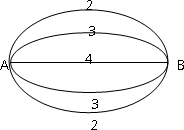
 如图,A、B两点有5条连线并联,它们在单位时间内通过的信息量依次为2,3,4,3,2.现在任取三条线且记在单位时间内通过的信息总量为ξ.
如图,A、B两点有5条连线并联,它们在单位时间内通过的信息量依次为2,3,4,3,2.现在任取三条线且记在单位时间内通过的信息总量为ξ.
