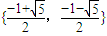题目内容
若在直线l上存在不同的三个点A,B,C,使得关于实数的方程x2
+x
+
=
有解(点O不在l上),则此方程的解集为( )
| OA |
| OB |
| BC |
| 0 |
| A.{-1} | B.{0} | ||||||||
C.{
| D.{-1,0} |
x2
+x
+
=
即x2
+x
+
-
=
∴-x2
-x
+
=
∵A,B,C共线
∴-x2-x+1=1解得x=0,-1
当x=0时,x2
+x
+
=
等价于
=
不合题意
故选A.
| OA |
| OB |
| BC |
| 0 |
即x2
| OA |
| OB |
| OC |
| OB |
| 0 |
∴-x2
| OA |
| OB |
| OB |
| OC |
∵A,B,C共线
∴-x2-x+1=1解得x=0,-1
当x=0时,x2
| OA |
| OB |
| BC |
| 0 |
| BC |
| 0 |
故选A.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
若在直线l上存在不同的三个点A,B,C,使得关于实数x的方程x2
+x
+
=
有解(点O不在l上),则此方程的解集为( )
| OA |
| OB |
| BC |
| 0 |
| A、{-1} | ||||||||
| B、{0} | ||||||||
C、{
| ||||||||
| D、{-1,0} |
 0有解(点O不在l上),则此方程的解集为
0有解(点O不在l上),则此方程的解集为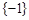 (B)
(B)
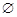
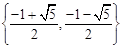 (D)
(D)
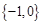
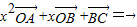 有解(点O不在l上),则此方程的解集为( )
有解(点O不在l上),则此方程的解集为( )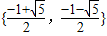
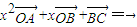 有解(点O不在l上),则此方程的解集为( )
有解(点O不在l上),则此方程的解集为( )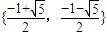
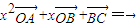 有解(点O不在l上),则此方程的解集为( )
有解(点O不在l上),则此方程的解集为( )