题目内容
已知数列{an}的首项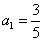 ,
,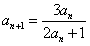 ,n=1,2,…。
,n=1,2,…。
(1)求{an}的通项公式;
(2)证明:对任意x>0,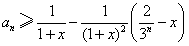 ,n=1,2,…。
,n=1,2,…。
(3)证明:a1+a2+…+an>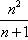 。
。
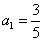 ,
,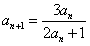 ,n=1,2,…。
,n=1,2,…。(1)求{an}的通项公式;
(2)证明:对任意x>0,
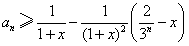 ,n=1,2,…。
,n=1,2,…。(3)证明:a1+a2+…+an>
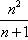 。
。解:(1)∵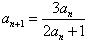
∴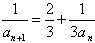
∴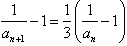
又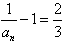
∴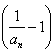 是以
是以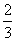 为首项,
为首项,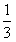 公比的等比数列
公比的等比数列
∴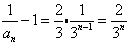
∴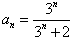 。
。
(2)由(1)知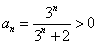
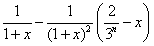
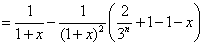
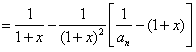
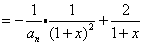
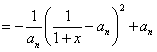
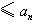
∴原不等式成立。
(3)由(2)知,对任意的x>0,有
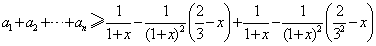
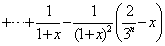
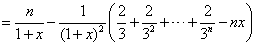
∴取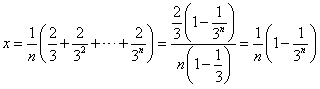
则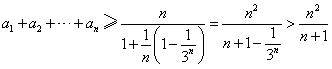
∴原式不等式成立。
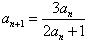
∴
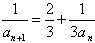
∴
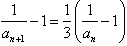
又
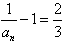
∴
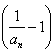 是以
是以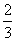 为首项,
为首项,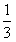 公比的等比数列
公比的等比数列∴
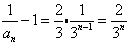
∴
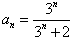 。
。(2)由(1)知
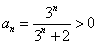
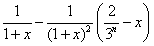
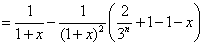
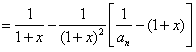
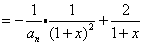
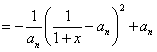
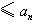
∴原不等式成立。
(3)由(2)知,对任意的x>0,有
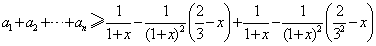
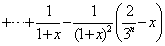
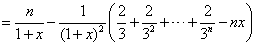
∴取
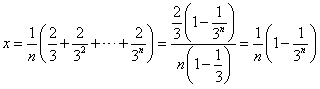
则
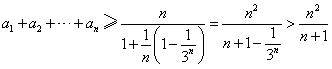
∴原式不等式成立。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目