题目内容
(2013•东莞二模)某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
(1)该同学为了求出y关于x的线性回归方程
=
x+
,根据表中数据已经正确计算出
=0.6,试求出
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊,后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ,求ξ的分布列和数学期望.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| y(万盒) | 4 | 4 | 5 | 6 | 6 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
 |
| a |
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊,后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ,求ξ的分布列和数学期望.
分析:(1)由线性回归方程过点(
,
),得
=
-
,而
,
易求,且
=0.6,从而可得
的值,把x=6代入回归方程可得6月份生产的甲胶囊产量数;
(2)ξ=0,1,2,3,利用古典概型的概率计算公式可得P(ξ=0)、P(ξ=1)、P(ξ=2)、P(ξ=3),从而可得ξ的分布列,由期望公式可求ξ的期望;
. |
| x |
. |
| y |
 |
| a |
. |
| y |
 |
| b |
. |
| x |
. |
| x |
. |
| y |
 |
| b |
 |
| a |
(2)ξ=0,1,2,3,利用古典概型的概率计算公式可得P(ξ=0)、P(ξ=1)、P(ξ=2)、P(ξ=3),从而可得ξ的分布列,由期望公式可求ξ的期望;
解答:解:(1)
=
(1+2+3+4+5)=3,
=
(4+4+5+6+6)=5,
因线性回归方程
=
x+
过点(
,
),
∴
=
-
=5-0.6×3=3.2,
∴6月份的生产甲胶囊的产量数:
=0.6×6+3.2=6.8.
(2)ξ=0,1,2,3,
P(ξ=0)=
=
,P(ξ=1)=
=
,
P(ξ=2)=
=
,P(ξ=3)=
=
,
其分布列为
所以Eξ=
×0+
×1+
×2+
×3=
.
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
因线性回归方程
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
∴
 |
| a |
. |
| y |
 |
| b |
. |
| x |
∴6月份的生产甲胶囊的产量数:
 |
| y |
(2)ξ=0,1,2,3,
P(ξ=0)=
| ||
|
| 5 |
| 42 |
| ||||
|
| 10 |
| 21 |
P(ξ=2)=
| ||||
|
| 5 |
| 14 |
| ||
|
| 1 |
| 21 |
其分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 5 |
| 42 |
| 10 |
| 21 |
| 5 |
| 14 |
| 1 |
| 21 |
| 4 |
| 3 |
点评:本题考查线性回归方程、离散型随机变量的分布列及其数学期望,考查学生分析解决问题的能力.

练习册系列答案
相关题目
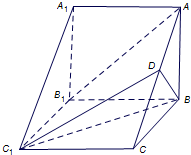 (2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.
(2013•东莞二模)如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.