题目内容
1.已知二次函数f(x)=x2+ax+b图象的对称轴为x=$\frac{1}{2}$,且f(1)=0,数列{an}满足an=f(2n+1)-f(2n)-1.(1)求数列{an}的前30项和;
(2)若am,at(m,t∈N*)是数列{an}中的项,试判断2am+3at是否是数列{an}中的项,并说明理由.
分析 (1)求得二次函数的对称轴方程,可得a=-1,再由f(1)=0,可得b=0,进而得到f(x),求得数列的通项公式,再由前n项和的公式,计算可得;
(2)由题意可得am=4m-1,at=4t-1,2am+3at=8m-2+12t-3=8m+12t-5=4(2m+3t-1)-1,由整数的性质,即可得到结论.
解答 解:(1)f(x)=x2+ax+b的对称轴为x=-$\frac{a}{2}$,
由题意可得a=-1,1+a+b=0,解得b=0,
则f(x)=x2-x,
即有an=f(2n+1)-f(2n)-1=(2n+1)2-(2n+1)-(2n)2+2n-1=4n-1,
则数列{an}的前30项和为$\frac{1}{2}$×(3+120-1)×30=1830;
(2)由题意可得am=4m-1,at=4t-1,
2am+3at=8m-2+12t-3=8m+12t-5
=4(2m+3t-1)-1,
由m,t∈N*,可得2m+3t-1∈N*,
即有2am+3at是数列{an}中的项.
点评 本题考查二次函数的对称轴和解析式,考查等差数列的求和公式的运用,同时考查通项公式的运用,以及整数的性质,考查运算和推理能力,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
9.以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角性”.

该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )

该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数为( )
| A. | 2017×22015 | B. | 2017×22014 | C. | 2016×22015 | D. | 2016×22014 |
6.过椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的焦点F作直线l交椭圆C于P,Q两点.若|FP|=p,|FQ|=q,则$\frac{1}{p}$+$\frac{1}{q}$=( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
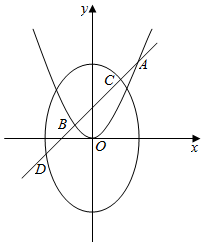 如图,抛物线C1:y=$\frac{1}{4}$x2的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且在两曲线的一个公共点处的直线l1:$\sqrt{6}$x-2y-3=0与C1相切.
如图,抛物线C1:y=$\frac{1}{4}$x2的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且在两曲线的一个公共点处的直线l1:$\sqrt{6}$x-2y-3=0与C1相切.