题目内容
(本题满分12分)
已知函数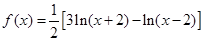 ,
,
(1)求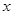 为何值时,
为何值时,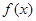 在
在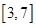 上取得最大值;
上取得最大值;
(2)设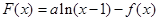 ,若
,若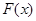 是单调递增函数,求
是单调递增函数,求 的取值范围.
的取值范围.
【答案】
(1)当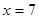 时,
时,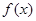 在
在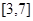 上取得最大值. (2)a的取值范围为
上取得最大值. (2)a的取值范围为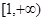
【解析】(1)利用导数研究其极值,然后与区间端点对应的函数值进行比较从而确定其最值.
(2) 本题的关键是把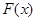 是单调递增的函数,转化为
是单调递增的函数,转化为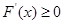 恒成立问题来解决.
恒成立问题来解决.
由于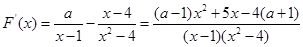 ,
,
显然在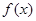 的定义域
的定义域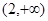 上,
上,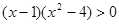 恒成立.
恒成立.
转化为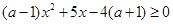 在
在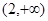 上恒成立.
上恒成立.
下面再对a进行讨论.
解:(1)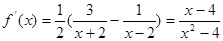
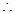 当
当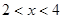 时,
时,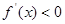 ;当
;当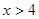 时,
时,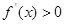 .
.
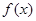 在
在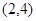 上是减函数,在
上是减函数,在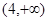 上是增函数.
上是增函数.
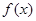 在
在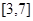 上的最大值应在端点处取得.
上的最大值应在端点处取得.
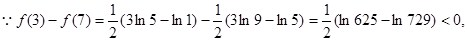
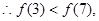 即当
即当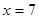 时,
时,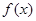 在
在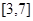 上取得最大值.………………5分
上取得最大值.………………5分
(2)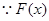 是单调递增的函数,
是单调递增的函数,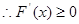 恒成立.
恒成立.
又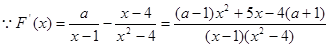 ,
,
显然在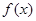 的定义域
的定义域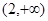 上,
上,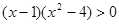 恒成立
恒成立
 ,在
,在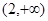 上恒成立.
上恒成立.
下面分情况讨论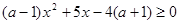 在
在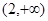 上恒成立时,
上恒成立时,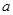 的解的情况
的解的情况
当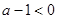 时,显然不可能有
时,显然不可能有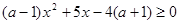 在
在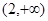 上恒成立;
上恒成立;
当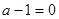 时,
时,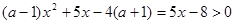 在
在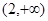 上恒成立;
上恒成立;
当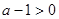 时,又有两种情况:
时,又有两种情况:
①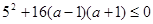 ;
;
②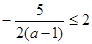 且
且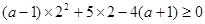
由①得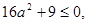 无解;由②得
无解;由②得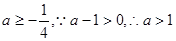
综上所述各种情况,当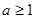 时,
时,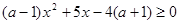 在
在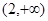 上恒成立
上恒成立
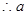 的取值范围为
的取值范围为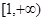 ……………………12分
……………………12分

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面