题目内容
设A1、A2与B分别是椭圆E:
+
=1(a>b>0)的左右顶点与上定点,直线A2B与圆C:x2+y2=1相切.
(1)求证:
+
=1;
(2)P是椭圆E上异于A1、A2 的一点,直线PA1、PA2的斜率之积为-
,求椭圆E的方程;
(3)直线l与椭圆E交于M、N两点,且
•
=0,试判断直线l与圆C的位置关系,并说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求证:
| 1 |
| a2 |
| 1 |
| b2 |
(2)P是椭圆E上异于A1、A2 的一点,直线PA1、PA2的斜率之积为-
| 1 |
| 3 |
(3)直线l与椭圆E交于M、N两点,且
| OM |
| ON |
分析:(1)由题设知A1(-a,0),A2(a,0),B(0,b),故直线A2B的方程是
+
=1,再由直线A2B与圆C:x2+y2=1相切,能够证明
+
=1.
(2)设P(x0,y0),则直线PA1,PA2的斜率之积为kPA1•kPA2=
•
=
=-
,由此能够求出椭圆E的方程.
(3)设点M(x1,y1),N(x2,y2),设直线l为y=kx+m,由y=kx+m代入
+
=1,得
+
=1,由此能够推导出直线l与圆C相切.若直线l的斜率不存在同样能够导出直线l与圆C相切.
| x |
| a |
| y |
| b |
| 1 |
| a2 |
| 1 |
| b2 |
(2)设P(x0,y0),则直线PA1,PA2的斜率之积为kPA1•kPA2=
| y0 |
| x0+a |
| y0 |
| x0-a |
| y02 |
| x02-a2 |
| 1 |
| 3 |
(3)设点M(x1,y1),N(x2,y2),设直线l为y=kx+m,由y=kx+m代入
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| (kx+m)2 |
| b2 |
解答:(1)证明:∵A1、A2与B分别是椭圆E:
+
=1(a>b>0)的左右顶点与上定点,
∴A1(-a,0),A2(a,0),B(0,b),
∴直线A2B的方程是
+
=1,
∵直线A2B与圆C:x2+y2=1相切,
∴
=1,故
+
=1.
(2)解:设P(x0,y0),则直线PA1,PA2的斜率之积为:
kPA1•kPA2=
•
=
=-
,
+
=1,
∵
+
=1,∴b2=
a2,
结合
+
=1,得a2=4,b2=
,
∴椭圆E的方程为
+
=1.
(3)解:设点M(x1,y1),N(x2,y2),
①若直线l的斜率存在,设直线l为y=kx+m,
由y=kx+m代入
+
=1,得
+
=1,
化简,得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0(△>0),
∴x1x2=
,
y1y2=(kx1+m)(kx2+m)
=k2x1x2+km(x1+x2)+m2
=
+km(-
)+m2
=
,
∵
•
=0,∴x1x2+y1y2=0.
代入,得(a2+b2)m2-a2b2(1+k2)=0,
∵
+
=1,∴m2=1+k2,
圆心到直线l的距离为d=
=1,
所以,直线l与圆C相切.
②若直线l的斜率不存在,设直线l:x=n,
代入
+
=1,得y=±b
,
∴|n|=b
,∴a2n2=b2(a2-n2),
化简整理可得n2=
,
又由(1)中的结论可知,
+
=1,即
=1,
∴n2=1,
解得n=±1,所以直线l与圆C相切.
| x2 |
| a2 |
| y2 |
| b2 |
∴A1(-a,0),A2(a,0),B(0,b),
∴直线A2B的方程是
| x |
| a |
| y |
| b |
∵直线A2B与圆C:x2+y2=1相切,
∴
| 1 | ||||||
|
| 1 |
| a2 |
| 1 |
| b2 |
(2)解:设P(x0,y0),则直线PA1,PA2的斜率之积为:
kPA1•kPA2=
| y0 |
| x0+a |
| y0 |
| x0-a |
| y02 |
| x02-a2 |
| 1 |
| 3 |
| x02 |
| a2 |
| 3y02 |
| a2 |
∵
| x02 |
| a2 |
| y02 |
| b2 |
| 1 |
| 3 |
结合
| 1 |
| a2 |
| 1 |
| b2 |
| 4 |
| 3 |
∴椭圆E的方程为
| x2 |
| 4 |
| 3y2 |
| 4 |
(3)解:设点M(x1,y1),N(x2,y2),
①若直线l的斜率存在,设直线l为y=kx+m,
由y=kx+m代入
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| (kx+m)2 |
| b2 |
化简,得(b2+a2k2)x2+2a2kmx+a2m2-a2b2=0(△>0),
∴x1x2=
| a2m2-a2b2 |
| b2+a2k2 |
y1y2=(kx1+m)(kx2+m)
=k2x1x2+km(x1+x2)+m2
=
| a2k2m2-a2b2k2 |
| b2+a2k2 |
| 2a2km |
| b2+a2k2 |
=
| b2m2-a2b2k2 |
| b2+a2k2 |
∵
| OM |
| ON |
代入,得(a2+b2)m2-a2b2(1+k2)=0,
∵
| 1 |
| a2 |
| 1 |
| b2 |
圆心到直线l的距离为d=
| |m| | ||
|
所以,直线l与圆C相切.
②若直线l的斜率不存在,设直线l:x=n,
代入
| x2 |
| a2 |
| y2 |
| b2 |
1-
|
∴|n|=b
1-
|
化简整理可得n2=
| a2b2 |
| a2+b2 |
又由(1)中的结论可知,
| 1 |
| a2 |
| 1 |
| b2 |
| a2b2 |
| a2+b2 |
∴n2=1,
解得n=±1,所以直线l与圆C相切.
点评:本题考查椭圆方程的求法,判断直线与椭圆的位置关系,具体涉及到椭圆的简单性质、直线与椭圆的位置关系,综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
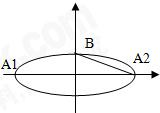 已知椭圆
已知椭圆
 ,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为
,A1、A2、B是椭圆的顶点(如图),直线l与椭圆交于异于椭圆顶点的P、Q两点,且l∥A2B.若此椭圆的离心率为 ,且
,且
