题目内容
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,PA=AD=1,E,F分别是AB、PD的中点.(1)求证:AF⊥平面PDC;
(2)求三棱锥B-PEC的体积;
(3)求证:AF∥平面PEC.

【答案】分析:(1)利用线面垂直的性质定理可得AB⊥AF.,再利用线面垂直的判定定理即可证明;
(2)利用三棱锥的体积计算公式VB-PEC=VP-BEC=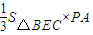 即可得出;
即可得出;
(3)取PC得中点M,连接MF、ME.利用三角形的中位线定理及矩形的性质可得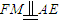 ,于是四边形AEMF是平行四边形,可得AF∥EM,再利用线面平行的判定定理可得AF∥平面PEC.
,于是四边形AEMF是平行四边形,可得AF∥EM,再利用线面平行的判定定理可得AF∥平面PEC.
解答:(1)证明:∵PA⊥平面ABCD,∴PA⊥CD,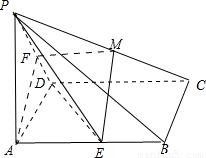
由底面ABCD是矩形,∴CD⊥DA,又PA∩AD=A,∴CD⊥平面PAD,
∴CD⊥AF.
∵PA=AD=1,F是PD的中点,
∴AF⊥PD,
又PD∩DC=D,∴AF⊥平面PDC.
(2)解: =
=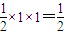 ,
,
∵PA⊥平面ABCD,
VB-PEC=VP-BEC=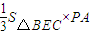 =
= .
.
(3)取PC得中点M,连接MF、ME.
∵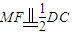 ,
,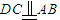 ,E是AB的中点,∴
,E是AB的中点,∴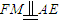 ,
,
∴四边形AEMF是平行四边形,
∴AF∥EM.
又AF?平面PEC,EM?平面PEC,
∴AF∥平面PEC.
点评:本题综合考查了线面垂直的判定与性质定理、线面与面面平行的判定与性质定理、三角形的中位线定理、平行四边形的性质、三棱锥的体积等基础知识与基本技能,考查了空间想象能力、推理能力和计算能力.
(2)利用三棱锥的体积计算公式VB-PEC=VP-BEC=
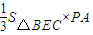 即可得出;
即可得出;(3)取PC得中点M,连接MF、ME.利用三角形的中位线定理及矩形的性质可得
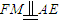 ,于是四边形AEMF是平行四边形,可得AF∥EM,再利用线面平行的判定定理可得AF∥平面PEC.
,于是四边形AEMF是平行四边形,可得AF∥EM,再利用线面平行的判定定理可得AF∥平面PEC.解答:(1)证明:∵PA⊥平面ABCD,∴PA⊥CD,

由底面ABCD是矩形,∴CD⊥DA,又PA∩AD=A,∴CD⊥平面PAD,
∴CD⊥AF.
∵PA=AD=1,F是PD的中点,
∴AF⊥PD,
又PD∩DC=D,∴AF⊥平面PDC.
(2)解:
 =
=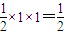 ,
,∵PA⊥平面ABCD,
VB-PEC=VP-BEC=
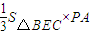 =
= .
.(3)取PC得中点M,连接MF、ME.
∵
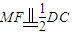 ,
,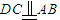 ,E是AB的中点,∴
,E是AB的中点,∴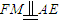 ,
,∴四边形AEMF是平行四边形,
∴AF∥EM.
又AF?平面PEC,EM?平面PEC,
∴AF∥平面PEC.
点评:本题综合考查了线面垂直的判定与性质定理、线面与面面平行的判定与性质定理、三角形的中位线定理、平行四边形的性质、三棱锥的体积等基础知识与基本技能,考查了空间想象能力、推理能力和计算能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
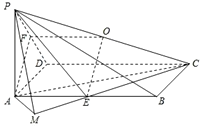 已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. (2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点.
(2012•即墨市模拟)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2a,AB=a,PA⊥平米ABCD,F是线段BC的中点.H为PD中点. 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ< (2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(2012•枣庄二模)已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.