题目内容
设等比数列{an}的公比q≠1,Sn表示数列{an}的前n项的和,Tn表示数列{an}的前n项的乘积,Tn(k)表示{an}的前n项中除去第k项后剩余的n-1项的乘积,即Tn(k)=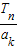 (n,k∈N+,k≤n),则数列
(n,k∈N+,k≤n),则数列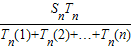 的前n项的和是 (用a1和q表示)
的前n项的和是 (用a1和q表示)
【答案】分析:由题设知 =
= ,Sn=
,Sn= ,故
,故 =
= ,由此能求出数列
,由此能求出数列 的前n项的和.
的前n项的和.
解答:解:∵等比数列{an}的公比q≠1,
Sn表示数列{an}的前n项的和,Tn表示数列{an}的前n项的乘积,
Tn(k)= (n,k∈N+,k≤n),
(n,k∈N+,k≤n),
∴
=
=
=
= ,
,
∵Sn= ,
,
∴ =
= ,
,
数列 的前n项的和
的前n项的和
S= [(1+q-q-1)+(1+q-q2-q-1)+(1+q-q3-q-2)+…+(1+q-qn-q1-n)]
[(1+q-q-1)+(1+q-q2-q-1)+(1+q-q3-q-2)+…+(1+q-qn-q1-n)]
= [n+nq-
[n+nq- -
- ]
]
= (n+nq-
(n+nq- ).
).
故答案为: (n+nq-
(n+nq- ).
).
点评:本题考查数列的前n项和的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
 =
= ,Sn=
,Sn= ,故
,故 =
= ,由此能求出数列
,由此能求出数列 的前n项的和.
的前n项的和.解答:解:∵等比数列{an}的公比q≠1,
Sn表示数列{an}的前n项的和,Tn表示数列{an}的前n项的乘积,
Tn(k)=
 (n,k∈N+,k≤n),
(n,k∈N+,k≤n),∴

=

=

=

=
 ,
,∵Sn=
 ,
,∴
 =
= ,
,数列
 的前n项的和
的前n项的和S=
 [(1+q-q-1)+(1+q-q2-q-1)+(1+q-q3-q-2)+…+(1+q-qn-q1-n)]
[(1+q-q-1)+(1+q-q2-q-1)+(1+q-q3-q-2)+…+(1+q-qn-q1-n)]=
 [n+nq-
[n+nq- -
- ]
]=
 (n+nq-
(n+nq- ).
).故答案为:
 (n+nq-
(n+nq- ).
).点评:本题考查数列的前n项和的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设等比数列{an}的前n项和为Sn,若
=3,则
=( )
| S6 |
| S3 |
| S9 |
| S6 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |