题目内容
7.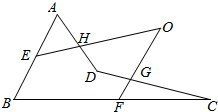 在空间四边形ABCD(四点不在一个平面上)的边AB、BC、CD、DA上分别取点E、F、G、H,若直线EH和直线FG相交于O点.求证:B、D、O三点共线.
在空间四边形ABCD(四点不在一个平面上)的边AB、BC、CD、DA上分别取点E、F、G、H,若直线EH和直线FG相交于O点.求证:B、D、O三点共线.
分析 根据公理1,可得直线EH?平面ABD,进而点O∈平面ABD,同理点O∈平面BCD,再由公理3可得:点O∈平面BCD∩平面ABD=BD
解答 证明:∵E,H∈平面ABD,
∴直线EH?平面ABD,
∵点O∈直线EH,
∴点O∈平面ABD,
∵F,G∈平面BCD,
∴直线FG?平面BCD,
∵点O∈直线FG,
∴点O∈平面BCD,
∴点O∈平面BCD∩平面ABD=BD,
即B、D、O三点共线
点评 本题考查的知知识点是平面的基本性质及推论,熟练掌握公理1和公理3是解答的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
18.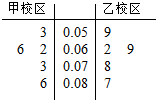 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,天津8.12爆炸事故后,天滓市环保部门对离爆炸点最近的甲、乙两所中学PM2.5进行监测,如图所示的是在开学前一天在甲、乙两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)的茎叶图,则关于甲、乙两个校区PM2.5浓度的方差,下列说法正确的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,天津8.12爆炸事故后,天滓市环保部门对离爆炸点最近的甲、乙两所中学PM2.5进行监测,如图所示的是在开学前一天在甲、乙两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)的茎叶图,则关于甲、乙两个校区PM2.5浓度的方差,下列说法正确的是( )
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,天津8.12爆炸事故后,天滓市环保部门对离爆炸点最近的甲、乙两所中学PM2.5进行监测,如图所示的是在开学前一天在甲、乙两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)的茎叶图,则关于甲、乙两个校区PM2.5浓度的方差,下列说法正确的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,天津8.12爆炸事故后,天滓市环保部门对离爆炸点最近的甲、乙两所中学PM2.5进行监测,如图所示的是在开学前一天在甲、乙两个校区附近的PM2.5监测点统计的数据(单位:毫克/立方米)的茎叶图,则关于甲、乙两个校区PM2.5浓度的方差,下列说法正确的是( )| A. | 甲校区较小 | B. | 乙校区较小 | ||
| C. | 甲乙两个校区相等 | D. | 无法确定 |
15.从某大学随机抽取的5名女大学生的身高x(厘米)和体重y(公斤)数据如表
根据上表可得回归直线方程为$\widehat{y}=0.92x+\widehat{a}$,则$\widehat{a}$=( )
| x | 165 | 160 | 175 | 155 | 170 |
| y | 58 | 52 | 62 | 43 | 60 |
| A. | -96.8 | B. | 96.8 | C. | -104.4 | D. | 104.4 |