题目内容
如图，在六面体ABCDEFG中，平面ABC∥平面DEFC，AD⊥平面DEFC，AB⊥AC，ED⊥DG，EF∥DC，且AB=AD=DE=DG=2，AC=EF=l，
(Ⅰ)求证：BF∥平面ACGD：
(Ⅱ)求二面角D-CC-F的余弦值；
(Ⅲ)求六面体ABCDEFG的体积。
(Ⅰ)求证：BF∥平面ACGD：
(Ⅱ)求二面角D-CC-F的余弦值；
(Ⅲ)求六面体ABCDEFG的体积。
| 解：由已知，AD，DE，DG两两垂直，建立如图的坐标系， 则  ， ，(Ⅰ)  ， ，∴  ，所以，  ，又  平面ACGD，故 平面ACGD。(Ⅱ)  ，设平面BCGF的法向量为  ，则  ，令y=2，则  ，而平面ADCG的法向量  ，∴  ，故二面角D-CG-F的余弦值为  。(Ⅲ)设DG的中点为M，连结AM，FM， 则    。 |
 |
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
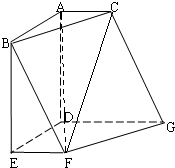如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG，且AC=EF=1，AB=AD=DE=DG=2．
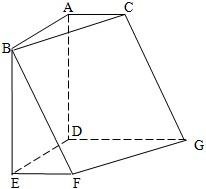如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG．且AB=AD=DE=DG=2，AC=EF=1．
如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG，且AC=EF=1，AB=AD=DE=DG=2．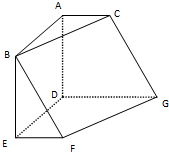
如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，ED⊥DG，EF∥DG．且AC=EF=1，AB=AD=DE=DG=2．
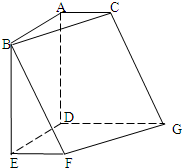如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG．且AB=AD=DE=DG=2，AC=EF=1．