题目内容
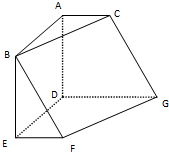如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，ED⊥DG，EF∥DG．且AC=EF=1，AB=AD=DE=DG=2．（1）求证：BF∥平面ACGD；
（2）求二面角D-CG-F的余弦值．
分析：（1）设DG的中点为M，连接AM、FM，证明BF平行平面ACGD内的直线AM，即可证明BF∥平面ACGD．
（2）过点M作MN⊥CG，N为垂足，则∠MNF为二面角D-CG-F的平面角．由题意求得 MN=
=
，FN=
=
，再由cos∠MNF=
，
运算求得结果．
（2）过点M作MN⊥CG，N为垂足，则∠MNF为二面角D-CG-F的平面角．由题意求得 MN=
| CM•MG |
| CG |
| 2 | ||
|
| FM2+MN2 |
2
| ||
| 5 |
| MN |
| FN |
运算求得结果．
解答：解：（1）设DG的中点为M，连接AM、FM，则由已知条件易证四边形DEFM是平行四边形，
所以MF∥DE，且MF=DE．
又∵AB∥DE，且AB=DE，∴MF∥AB，且MF=AB．
∴四边形ABMF是平行四边形，即BF∥AM，
又BF?平面ACGD 故BF∥平面ACGD．
（2）由AD⊥平面DEFG，可得AD⊥ED，再由ED⊥DG，可得ED⊥平面ACGD．由（1）四边形DEFM是平行四边形，
可得FM⊥平面ACGD，故有 FM⊥CG．
过点M作MN⊥CG，N为垂足，则∠MNF为二面角D-CG-F的平面角．
由题意可得，AD=CM=2，MG=1，CG=
=
，∴MN=
=
．
直角三角形FMN中，由勾股定理求得FN=
=
，∴cos∠MNF=
=
=
．
所以MF∥DE，且MF=DE．
又∵AB∥DE，且AB=DE，∴MF∥AB，且MF=AB．
∴四边形ABMF是平行四边形，即BF∥AM，
又BF?平面ACGD 故BF∥平面ACGD．
（2）由AD⊥平面DEFG，可得AD⊥ED，再由ED⊥DG，可得ED⊥平面ACGD．由（1）四边形DEFM是平行四边形，
可得FM⊥平面ACGD，故有 FM⊥CG．
过点M作MN⊥CG，N为垂足，则∠MNF为二面角D-CG-F的平面角．
由题意可得，AD=CM=2，MG=1，CG=
| CM2+MG2 |
| 5 |
| CM•MG |
| CG |
| 2 | ||
|
直角三角形FMN中，由勾股定理求得FN=
| FM2+MN2 |
2
| ||
| 5 |
| MN |
| FN |
| ||||
|
| ||
| 6 |
点评：题考查直线与平面平行的判定，求二面角的平面角，考查逻辑思维能力，空间想象能力，转化能力，是中档题．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
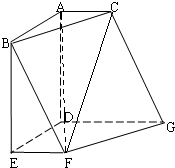如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG，且AC=EF=1，AB=AD=DE=DG=2．
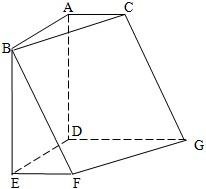如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG．且AB=AD=DE=DG=2，AC=EF=1．
如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG，且AC=EF=1，AB=AD=DE=DG=2．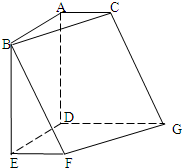
如图，在六面体ABCDEFG中，平面ABC∥平面DEFG，AD⊥平面DEFG，AB⊥AC，ED⊥DG，EF∥DG．且AB=AD=DE=DG=2，AC=EF=1．